题目内容
如图,已知AB是⊙O的弦,半径OA=6cm,∠AOB=120º,则AB= cm.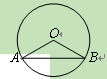


过O作OC⊥AB于C,根据等腰三角形的性质和三角形的内角和定理求出∠A,根据含30度得直角三角形性质求出OC,根据勾股定理求出AC,根据垂径定理求出即可.
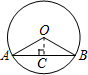
解:过O作OC⊥AB于C,
∵OA=OB,
∴∠A=∠B,
∵∠AOB=120°,
∴∠A=∠B=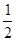 (180°-∠AOB)=30°,
(180°-∠AOB)=30°,
∴OC=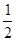 OA=3,
OA=3,
由勾股定理得:AC=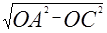 =3
=3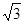 ,
,
∵OC⊥AB,OC过圆心O,
∴AC=BC,
∴AB=2AC=6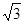 ,
,
故答案为:6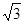 .
.
本题主要考查对三角形的内角和定理,勾股定理,等腰三角形的性质,垂径定理,含30度角的直角三角形等知识点的理解和掌握,能求出OC、AC的长是解此题的关键.

解:过O作OC⊥AB于C,
∵OA=OB,
∴∠A=∠B,
∵∠AOB=120°,
∴∠A=∠B=
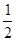 (180°-∠AOB)=30°,
(180°-∠AOB)=30°,∴OC=
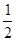 OA=3,
OA=3,由勾股定理得:AC=
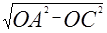 =3
=3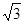 ,
,∵OC⊥AB,OC过圆心O,
∴AC=BC,
∴AB=2AC=6
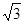 ,
,故答案为:6
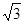 .
.本题主要考查对三角形的内角和定理,勾股定理,等腰三角形的性质,垂径定理,含30度角的直角三角形等知识点的理解和掌握,能求出OC、AC的长是解此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的切线,切点为
的切线,切点为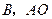 交
交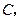 过点
过点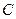 作
作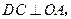 交
交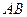 于点
于点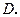
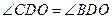 ;
;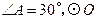 的半径为4,求CD的长;
的半径为4,求CD的长;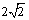 的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。
的圆经过一个半径为4的圆的圆心,则图中阴影部分的面积为 。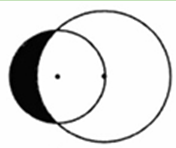
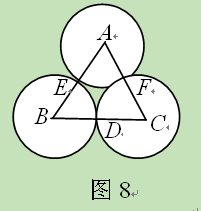
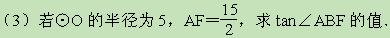 .
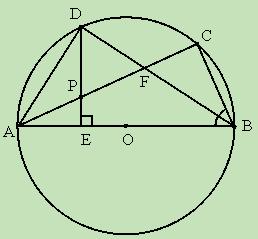
.
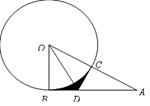
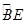 是半径为 6 的⊙D的
是半径为 6 的⊙D的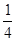 圆周,C点是
圆周,C点是
 ,点O是这条弧所在圆的圆心,点C是
,点O是这条弧所在圆的圆心,点C是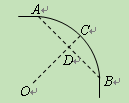
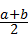 与
与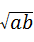 的大小关系是
的大小关系是 ●探究证明
●探究证明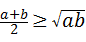 .
. ,∠COD=60°.
,∠COD=60°.