题目内容
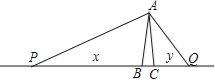
【题目】如图,在△ABC中,AB=AC=2,∠BAC=20°.动点P、Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )
A. B.
B. C.
C. D.
D.
【答案】A
【解析】
试题根据题意,需得出x与y的关系式,也就是PB与CQ的关系,
∵AB=AC=2,∠BAC=20°
∴△ABC是等腰三角形,∠ABC=∠ACB,又∵三角形内角和是180°
∴∠ABC=(180°-∠BAC)÷2=80°
∵三角形的外角等于与其不相邻的两个内角之和∴∠PAB+∠P=∠ABC
即∠P+∠PAB=80°,
又∵∠BAC=20°,∠PAQ=100°,
∴∠PAB+∠QAC=80°,
∴∠P=∠QAC,
同理可证
∠PAB=∠Q,
∴△PAB∽△AQC,
∴![]() , 代入得
, 代入得![]()
得出,y与x的关系式![]() ,由此可知,这是一个反比例函数,只有选项A的图像是反比例函数的图像.
,由此可知,这是一个反比例函数,只有选项A的图像是反比例函数的图像.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克) | 7 | 5 |
价格y(千克) | 2000 | 4000 |
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?