Question

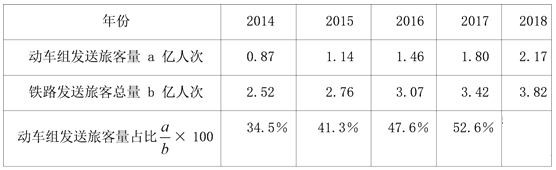
【题目】如图，⊙O的内接四边形ABCD中，AC，BD是它的对角线，AC的中点I是△ABD的内心．求证：

（1）OI是△IBD的外接圆的切线；

（2）AB+AD＝2BD．

Answer 1

【答案】(1)证明见解析；(2)证明见解析.

【解析】

（1）根据三角形内心的性质和同弧上圆周角的性质，以及等角对等边即可证得C是△IBD的外心，然后证得OI⊥CI，即可证得OI是△IBD的外接圆的切线；

（2）根据（1）可以得到AI=CD，AB=2BF，即可证得．

(1)∵∠CID=∠IAD+∠IDA，∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA

∴∠CID=∠CDI，

∴CI=CD．

同理，CI=CB．

故点C是△IBD的外心．

连接OA，OC，

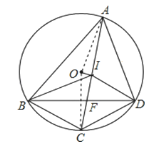
∵I是AC的中点，且OA=OC，

∴OI⊥AC，即OI⊥CI．

∴OI是△IBD外接圆的切线．

(2)由(1)可得：

∵AC的中点I是△ABD的内心，

∴∠BAC=∠CAD

∴∠BDC=∠DAC=∠BAC，

又∵∠ACD=∠DCF，

∴△ADC∽△DFC，

∴，

∵AC=2CI

∴AC=2CD

∴AD=2DF

同理可得：AB=2BF

∴AB+AD=2BF+2DF=2BD．