Question

【题目】已知抛物线与轴交于两点，与轴交于点．

（1）求的取值范围；

（2）若，直线经过点，与轴交于点，且，求抛物线的解析式；

（3）若点在点左边，在第一象限内，（2）中所得到抛物线上是否存在一点，使直线分的面积为两部分？若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）m≠-2；（2）y=-x2+5x-6；（3）点P（，-）或（2，0）．

【解析】

（1）由于抛物线与x轴有两个不同的交点，可令y=0，则所得方程的根的判别式△＞0，可据此求出m的取值范围．
（2）根据已知直线的解析式，可得到D点的坐标；根据抛物线的解析式，可用m表示出A、B的坐标，即可得到AD、BD的长，代入AD×BD=5，即可求得m的值，从而确定抛物线的解析式．
（3）直线PA分△ACD的面积为1：4两部分，即DH：HC=1：4或4：1，则点H（0，-2）或（0，-5），即可求解．

解：（1）∵抛物线与x轴有两个不同的交点，
∴△=（m-4）2+12（m-1）=m2+4m+4=（m+2）2＞0，
∴m≠-2．
（2）∵y=-x2-（m-4）x+3（m-1）=-（x-3）（x+m-1），
∴抛物线与x轴的两个交点为：（3，0），（1-m，0）；
则：D（0，-1），
则有：AD×BD=，
解得：m=2（舍去）或-1，
∴m=-1，
抛物线的表达式为：y=-x2+5x-6①；
（3）存在，理由：
如图所示，点C（0，-6），点D（0，-1），点A（2，0），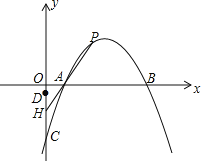

直线PA分△ACD的面积为1：4两部分，
即DH：HC=1：4或4：1，则点H（0，-2）或（0，-5），
将点H、A的坐标代入一次函数表达式并解得：
直线HA的表达式为：y=x-2或y=x-5②，
联立①②并解得：x=或2，
故点P（，-）或（2，0）．