题目内容
【题目】如图,一次函数 ![]() (
( ![]() )与反比例函数
)与反比例函数 ![]() (
( ![]() )的图象交于点
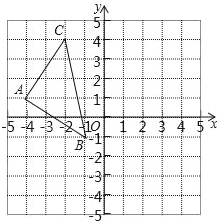
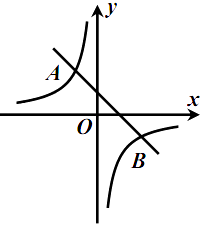
)的图象交于点 ![]() ,
, ![]() .
.
(1)求这两个函数的表达式;
(2)在 ![]() 轴上是否存在点
轴上是否存在点 ![]()
![]() ,使
,使 ![]() 为等腰三角形?若存在,求
为等腰三角形?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(1)
解:把A(-1,2)代入y=![]() ,得k2=-2,
,得k2=-2,
∴反比例函数的表达式为y=![]() 。
。
∵B(m,-1)在反比例函数的图象上,
∴m=2。
由题意得![]() ,解得
,解得![]()
∴一次函数的表达式为y=-x+1。
(2)
解:由A(-1,2)和B(2,-1),则AB=3![]()
①当PA=PB时,(n+1)2+4=(n-2)2+1,
∵n>0,∴n=0(不符合题意,舍去)
②当AP=AB时,22+(n+1)2=(3![]() )2
)2
∵n>0,∴n=-1+![]()
③当BP=BA时,12+(n-2)2=(3![]() )2
)2
∵n>0,∴n=2+![]()
所以n=-1+![]() 或n=2+
或n=2+![]() 。
。
【解析】(1)将点A代入反比例函数解析式可先求出k2,再求出点B的坐标,再运用待定系数法求k1和b的值;
(2)需要分类讨论,PA=PB,AP=AB,BP=BA,运用勾股定理求它们的长,构造方程求出n的值.

练习册系列答案
相关题目
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
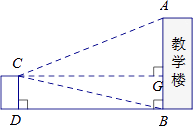
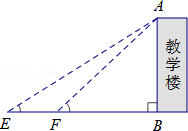
方案 | 一 | 二 |
图示 |
|
|
测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
参考数据 | sin22°≈0.37,cos22°≈0.93, | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)