Question

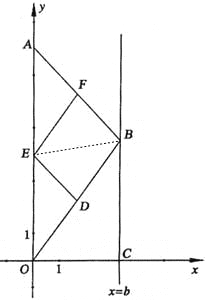
【题目】如图，在直角坐标系中，点A的坐标为（0，8），点 B（b，t）在直线x=b上运动，点D、E、F分别为OB、0A、AB的中点，其中b是大于零的常数．

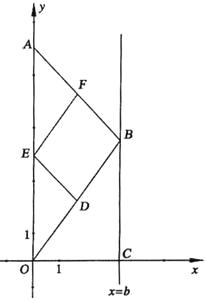
（1）判断四边形DEFB的形状．并证明你的结论；

（2）试求四边形DEFB的面积S与b的关系式；

（3）设直线x=b与x轴交于点C，问：四边形DEFB能不能是矩形？若能．求出t的值；若不能，说明理由．

Answer 1

【答案】（1）平行四边形，证明见解析；（2）S=2b（b＞0）；（3）当0＜b≤4时，四边形DEFB是矩形，这时，t=4±，当b＞4时，四边形DEFB不是矩形．

【解析】

解：（1）四边形DEFB是平行四边形．

证明：∵D、E分别是OB、OA的中点，

∴DE∥AB，同理，EF∥OB，

∴四边形DEFB是平行四边形；

（2）如图，连接BE，

S△AOB=×8×b=4b，

∵E、F分别为OA、AB的中点，

∴S△AEF=S△AEB=S△AOB=b，

同理S△EOD=b，

∴S=S△AOB-S△AEF-S△ODE=4b-b-b=2b，

即S=2b（b＞0）；

（3）解法一：以E为圆心，OA长为直径的圆记为⊙E，

①当直线x=b与⊙E相切或相交时，若点B是切点或交点，则∠ABO=90°，由（1）知，四边形DEFB是矩形，

此时0＜b≤4，可得△AOB∽△OBC，

∴

，即OB2=OABC=8t，

在Rt△OBC中，OB2=BC2+OC2=t2+b2，

∴t2+b2=8t，

∴t2-8t+b2=0，

解得t=4±，

②当直线x=b与⊙E相离时，∠ABO≠90°，

∴四边形DEFB不是矩形，

综上所述：当0＜b≤4时，四边形DEFB是矩形，这时，t=4±，当b＞4时，四边形DEFB不是矩形；

解法二：由（1）知，当∠ABO=90°时，四边形DEFB是矩形，

此时，Rt△OCB∽Rt△ABO，

∴，即OB2=OABC，

又OB2=BC2+OC2=t2+b2，OA=8，BC=t（t＞0），

∴t2+b2=8t，

∴（t-4）2=16-b2，

①当16-b2≥0时，解得t=4±，此时四边形DEFB是矩形，

②当16-b2＜0时，t无实数解，此时四边形DEFB不是矩形，

综上所述：当16-b2≥0时，四边形DEFB是矩形，此时t=4±，当16-b2＜0时，四边形DEFB不是矩形；

解法三：如图，过A作AM⊥BC，垂足为M，

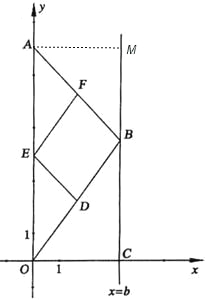
在Rt△AMB中，AB2=AM2+BM2=b2+（8-t）2，

在Rt△OCB中，OB2=OC2+BC2=b2+t2，

在Rt△OAB中，当AB2+OB2=OA2时，∠ABO=90°，则四边形DEFB为矩形，

∴b2+（8-t）2+b2+t2=82，

化简得t2-8t=-b2，配方得（t-4）2=16-b2，其余同解法二．