ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃЌ![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯвЛЕуЃЌвд
ЩЯвЛЕуЃЌвд![]() ЮЊЖЅЕузі
ЮЊЖЅЕузі![]() ЃЎ
ЃЎ ![]() НЛЙ§
НЛЙ§![]() ЧвЦНаагк
ЧвЦНаагк![]() ЕФжБЯпгк
ЕФжБЯпгк![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛЕБ
ЃЛЕБ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЪБЃЌЃЈШчЭМ1ЃЉаЁУїЭЌбЇКмПьОЭжЄУїСЫНсТлЃКЫћЕФзіЗЈЪЧЃКШЁ
ЕФжаЕуЪБЃЌЃЈШчЭМ1ЃЉаЁУїЭЌбЇКмПьОЭжЄУїСЫНсТлЃКЫћЕФзіЗЈЪЧЃКШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌШЛКѓжЄУї
ЃЌШЛКѓжЄУї![]() ЃЎ ДгЖјЕУЕН
ЃЎ ДгЖјЕУЕН![]() ЃЌЮвУЧМЬајРДбаОПЃК
ЃЌЮвУЧМЬајРДбаОПЃК
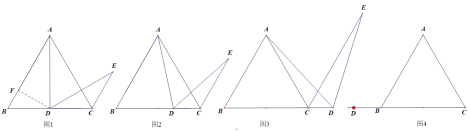
ЃЈ1ЃЉШчЭМ2ЁЂЕБDЪЧBCЩЯЕФШЮвтвЛЕуЪБЃЌЧѓжЄЃК![]()
ЃЈ2ЃЉШчЭМ3ЁЂЕБDдкBCЕФбгГЄЯпЩЯЪБЃЌЧѓжЄЃК![]()
ЃЈ3ЃЉЕБ![]() дк
дк![]() ЕФбгГЄЯпЩЯЪБЃЌЧыРћгУЭМ4ЛГіЭМаЮЃЌВЂЫЕУїЩЯУцЕФНсТлЪЧЗёГЩСЂЃЈВЛБижЄУїЃЉЃЎ
ЕФбгГЄЯпЩЯЪБЃЌЧыРћгУЭМ4ЛГіЭМаЮЃЌВЂЫЕУїЩЯУцЕФНсТлЪЧЗёГЩСЂЃЈВЛБижЄУїЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ4ЃЉМћНтЮіЃЌ![]() ЃЌШдГЩСЂ
ЃЌШдГЩСЂ
ЁОНтЮіЁП
ЃЈ1ЃЉдкABЩЯНиШЁAF=DCЃЌСЌНгFDЃЌжЄУїЁїBDFЪЧЕШБпШ§НЧаЮЃЌЕУГіЁЯBFD=60ЁуЃЌжЄГіЁЯFAD=ЁЯCDEЃЌгЩASAжЄУїЁїAFDЁеЁїDCEЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉдкBAЕФбгГЄЯпЩЯНиШЁAF=DCЃЌСЌНгFDЃЌжЄУїЁїBDFЪЧЕШБпШ§НЧаЮЕУГіЁЯF=60ЁуЃЌжЄГіЁЯFAD=ЁЯCDEЃЌгЩASAжЄУїЁїAFDЁеЁїDCEЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉдкABЕФбгГЄЯпЩЯНиШЁAF=DCЃЌСЌНгFDЃЌжЄУїЁїBDFЪЧЕШБпШ§НЧаЮЃЌЕУГіЁЯBFD=60ЁуЃЌжЄГіЁЯFAD=ЁЯCDEЃЌгЩASAжЄУїЁїAFDЁеЁїDCEЃЌМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉжЄУїЃКдкABЩЯНиШЁAF=DCЃЌСЌНгFDЃЌШчЭМЫљЪОЃК
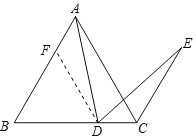
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=BCЃЌЁЯB=60ЁуЃЌ
гжЁпAF=DCЃЌ
ЁрBF=BDЃЌ
ЁрЁїBDFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBFD=60ЁуЃЌ
ЁрЁЯAFD=120ЁуЃЌ
гжЁпABЁЮCEЃЌ
ЁрЁЯDCE=120Ёу=ЁЯAFDЃЌ
ЖјЁЯEDC+ЁЯADE=ЁЯADC=ЁЯFAD+ЁЯBЁЯADE=ЁЯB=60ЁуЃЌ
ЁрЁЯFAD=ЁЯCDEЃЌ
дкЁїAFDКЭЁїDCEжа
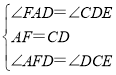 ЃЌ
ЃЌ
ЁрЁїAFDЁеЁїDCEЃЈASAЃЉЃЌ
ЁрAD=DEЃЛ
ЃЈ2ЃЉжЄУїЃКдкBAЕФбгГЄЯпЩЯНиШЁAF=DCЃЌСЌНгFDЃЌШчЭМЫљЪОЃК
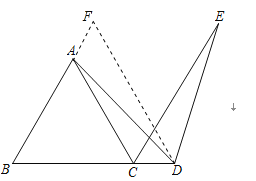
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=BCЃЌЁЯB=60ЁуЃЌ
гжЁпAF=DCЃЌ
ЁрBF=BDЃЌ
ЁрЁїBDFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯF=60ЁуЃЌ
гжЁпABЁЮCEЃЌ
ЁрЁЯDCE=60Ёу=ЁЯFЃЌ
ЖјЁЯFAD=ЁЯB+ЁЯADBЃЌЁЯCDE=ЁЯADE+ЁЯADBЃЌ
гжЁпЁЯADE=ЁЯB=60ЁуЃЌ
ЁрЁЯFAD=ЁЯCDEЃЌ
дкЁїAFDКЭЁїDCEжаЃЌ
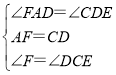 ЃЌ
ЃЌ
ЁрЁїAFDЁеЁїDCEЃЈASAЃЉЃЌ
ЁрAD=DEЃЛ
ЃЈ3ЃЉНтЃКAD=DEШдГЩСЂЃЎРэгЩШчЯТЃК
дкABЕФбгГЄЯпЩЯНиШЁAF=DCЃЌСЌНгFDЃЌШчЭМЫљЪОЃК
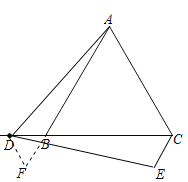
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=BCЃЌЁЯABC=60ЁуЃЌ
ЁрЁЯFAD+ЁЯADB=60ЁуЃЌ
гжЁпAF=DCЃЌ
ЁрBF=BDЃЌ
ЁпЁЯDBF=ЁЯABC=60ЁуЃЌ
ЁрЁїBDFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯAFD=60ЁуЃЌ
гжЁпABЁЮCEЃЌ
ЁрЁЯDCE=ЁЯABC=60ЁуЃЌ
ЁрЁЯAFD=ЁЯDCEЃЌ
ЁпЁЯADE=ЁЯCDE+ЁЯADB=60ЁуЃЌ
ЁрЁЯFAD=ЁЯCDEЃЌ
дкЁїAFDКЭЁїDCEжаЃЌ
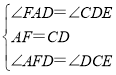 ЃЌ
ЃЌ
ЁрЁїAFDЁеЁїDCEЃЈASAЃЉЃЌ
ЁрAD=DEЃЎ

ЁОЬтФПЁПвЛаюЫЎГигаЫЎ40m3ЃЌАДвЛЖЈЕФЫйЖШЗХЫЎЃЌЫЎГиРяЕФЫЎСПyЃЈm3ЃЉгыЗХЫЎЪБМфtЃЈЗжЃЉгаШчЯТЙиЯЕЃК
ЗХЫЎЪБМфЃЈЗжЃЉ | 1 | 2 | 3 | 4 | Ё |
ЫЎГижаЫЎСПЃЈm3ЃЉ | 38 | 36 | 34 | 32 | Ё |
ЯТСаНсТлжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. yЫцtЕФдіМгЖјдіДѓ
B. ЗХЫЎЪБМфЮЊ15ЗжжгЪБЃЌЫЎГижаЫЎСПЮЊ8m3
C. УПЗжжгЕФЗХЫЎСПЪЧ2m3
D. yгыtжЎМфЕФЙиЯЕЪНЮЊyЃН40t
ЁОЬтФПЁПвЛВшвЖзЈТєЕъОЯњФГжжЦЗХЦЕФВшвЖЃЌИУВшвЖЕФГЩБОМлЪЧ80дЊ/kgЃЌЯњЪлЕЅМлВЛЕЭгк120дЊ/kgЃЎЧвВЛИпгк180дЊ/kgЃЌОЯњвЛЖЮЪБМфКѓЕУЕНШчЯТЪ§ОнЃК
ЯњЪлЕЅМлxЃЈдЊ/kgЃЉ | 120 | 130 | Ё | 180 |
УПЬьЯњСПyЃЈkgЃЉ | 100 | 95 | Ё | 70 |
ЩшyгыxЕФЙиЯЕЪЧЮвУЧЫљбЇЙ§ЕФФГвЛжжКЏЪ§ЙиЯЕЃЎ
ЃЈ1ЃЉжБНгаДГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂжИГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйЪБЃЌЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП




