题目内容
【题目】如图1,在平面直角坐标系中,已知点![]() ,以O为圆心,OA为半径作
,以O为圆心,OA为半径作![]() ,交y轴于点C,直线l:
,交y轴于点C,直线l:![]() 经过点C.
经过点C.
![]() 设直线l与
设直线l与![]() 的另一个交点为
的另一个交点为![]() 如图
如图![]() ,求弦CD的长;
,求弦CD的长;
![]() 将直线l向上平移2个单位,得直线m,如图2,求证:直线m与
将直线l向上平移2个单位,得直线m,如图2,求证:直线m与![]() 相切;
相切;
![]() 在
在![]() 的前提下,设直线m与
的前提下,设直线m与![]() 切于点P,Q为
切于点P,Q为![]() 上一动点,过点P作
上一动点,过点P作![]() ,交直线QA于点
,交直线QA于点![]() 如图
如图![]() ,则
,则![]() 的最大面积为______.
的最大面积为______.

【答案】![]() ;
;![]() 证明见解析;
证明见解析;![]() 54.
54.
【解析】
![]() 过点O作
过点O作![]() ,垂足为E,设直线l与x轴交于点B,利用面积法求出OE,再利用勾股定理求出CE即可解决问题;
,垂足为E,设直线l与x轴交于点B,利用面积法求出OE,再利用勾股定理求出CE即可解决问题;
![]() 过点O作
过点O作![]() ,垂足为F,设直线m与x轴交于点N,与y轴交于点M,
,垂足为F,设直线m与x轴交于点N,与y轴交于点M,![]() 如图
如图![]() ,只要证明
,只要证明![]() 半径即可解决问题;
半径即可解决问题;
![]() 设
设![]() 与x轴的另一交点为G,连接PA、OP、PG,过点P作
与x轴的另一交点为G,连接PA、OP、PG,过点P作![]() 轴于H,
轴于H,![]() 如图
如图![]() ,由
,由![]() ≌
≌![]() ,推出
,推出![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,推出当PQ取得最大值时,即
,推出当PQ取得最大值时,即![]() 时,
时,![]() 取得最大值.
取得最大值.
![]() 解:过点O作
解:过点O作![]() ,垂足为E,设直线l与x轴交于点B,
,垂足为E,设直线l与x轴交于点B,![]() 如图
如图![]()
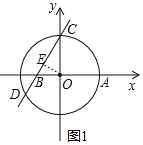
![]() 直线l:
直线l:![]() 经过点
经过点![]() ,
,
![]() ,直线l为
,直线l为![]() ,
,
由![]() 得,
得,![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 证明:过点O作
证明:过点O作![]() ,垂足为F,设直线m与x轴交于点N,与y轴交于点M,
,垂足为F,设直线m与x轴交于点N,与y轴交于点M,![]() 如图
如图![]()

![]() 直线m由直线l向上平移2个单位得到,
直线m由直线l向上平移2个单位得到,
![]() 直线m为
直线m为![]() ,
,
由![]() 得
得![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线m与
直线m与![]() 相切.
相切.
![]() 的最大面积为54.
的最大面积为54.
理由:设![]() 与x轴的另一交点为G,连接PA、OP、PG,过点P作
与x轴的另一交点为G,连接PA、OP、PG,过点P作![]() 轴于H,
轴于H,![]() 如图
如图![]()
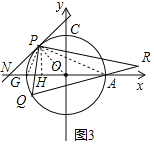
由![]() ∽
∽![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 当PQ取得最大值时,即
当PQ取得最大值时,即![]() 时,
时,![]() 取得最大值,
取得最大值,
此时![]() .
.
故答案为54.

练习册系列答案
相关题目