��Ŀ����
����Ŀ����5������ֱ�������֩�2����1��0��1��2�IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ����ÿ�Ƭ�ϵ����ּ�Ϊa��
(1)��a��0�ĸ��ʣ�
(2)���ʹ����x��һ�κ���y����a+1��x+a��4��ͼ�����ڶ����ޣ���ʹ����x�ķ���![]() +3=
+3=![]() ��������ĸ��ʣ�
��������ĸ��ʣ�
(3)���ٴ�ʣ�µ���������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊb����ʹһԪ���η���x2+2ax+b2��0��������Ϊ�����ĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
��������
��1�����ݸ��ʹ�ʽ���ɵõ����ۣ�
��2������ʹ�ù���x�ķ�ʽ����![]() �������⣬�ҹ���x��һ�κ���y=��a+1��x+a-4��ͼ�����ڶ���������Ȼ��ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
�������⣬�ҹ���x��һ�κ���y=��a+1��x+a-4��ͼ�����ڶ���������Ȼ��ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��3��������״ͼ��������ʹ�ʽ���㼴�ɣ�
�⣺��1��a��0�ĸ��ʣ�![]() ��
��
��2���⣺�߹���x�ķ�ʽ����![]() �������⣬
�������⣬
��3��ax+3��x��3������x��
��ã�x�� ![]() ��
��
��x��3��
��a��2��
�൱a����2��1ʱ����ʽ����![]() �������⣻
�������⣻
�߹���x��һ�κ���y����a+1��x+a��4��ͼ�����ڶ����ޣ�
��a+1��0��a��4��0��
����1��a��4��
�൱a��0��1��2��ʱ������x��һ�κ���y����a+1��x+a��4��ͼ�����ڶ����ޣ�
���ϣ���a��1ʱ��ʹ�ù���x�ķ�ʽ����![]() �������⣬�ҹ���x��һ�κ���y����a+1��x+a��4��ͼ�����ڶ����ޣ�
�������⣬�ҹ���x��һ�κ���y����a+1��x+a��4��ͼ�����ڶ����ޣ�
��ʹ�ù���x�ķ�ʽ����![]() �������⣬�ҹ���x��һ�κ���y����a+1��x+a��4��ͼ�����ڶ����ĸ����ǣ�
�������⣬�ҹ���x��һ�κ���y����a+1��x+a��4��ͼ�����ڶ����ĸ����ǣ�![]() ��
��
��3����һԪ���η���x2+2ax+b2��0��������Ϊ������
��x1+x2����2a��0��x1x2��b2��0������4a2��4b2��4��a+b����a��b����0
��a��0��b��0����|a|��|b|
����״ͼ��ͼ��ʾ��
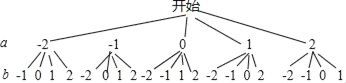
�߹���20�ֵȿ��ܽ��������ʹһԪ���η���x2+2ax+b2��0��������Ϊ��������4�������
��P��![]() ��
��