题目内容
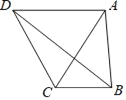
【题目】如图,在四边形ABCD中,AB=6,BC=4,若AC=AD,且∠ACD=60°,则对角线BD的长的最大值为_____.
【答案】10
【解析】
在AB的左侧作等边三角形△ABK,连接DK.由△DAK≌△CAB,推出DK=BC=4,因为DK+KB≥BD,DK=4,KB=AB=6,所以当D、K、B共线时,BD的值最大,最大值为DK+KB=10.
如图,在AB的左侧作等边三角形△ABK,连接DK,

则AK=AB=BK=6,∠KAB=60°,
∴∠DAC=∠KAB,
∴∠DAK=∠CAB,
在△DAK和△CAB中,
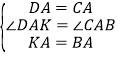 ,
,
∴△DAK≌△CAB(SAS)
∴DK=BC=4,
∵DK+KB≥BD,DK=4,KB=AB=6
∴当D、K、B共线时,BD的值最大,最大值为DK+KB=10.
故答案为:10

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目