Question

【题目】如图，平行四边形ABCD中，E是AD上的一点，且AE= AD，对角线AC，BD交于点O，EC交BD于F，BE交AC于G，如果平行四边形ABCD的面积为S，那么，△GEF的面积为（ ）
A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：过A作AM⊥BC于M，如图所示：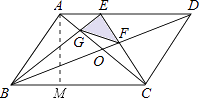
∵S△BEC= BCAM，SABCD=BCAM，
∴S△BEC= SABCD= S，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠EAG=∠BCG，∠AEG=∠CBG，
∴△AEG∽△CBG，又AE= AD= BC，
∴ = = ，
∴S△EFG= S△BGF ，
又S△EFG+S△BGF=S△BEF ，
∴S△EFG= S△BEF ，
∵AE= AD，AD=AE+ED，
∴ED= AD= BC，
同理得到△EFD∽△CFB，
∴ = = ，
∴S△BEF= S△BFC ，
又S△BEF+S△BFC=S△BEC ，
∴S△BEF= S△BEC= S，
∴S△EFG= S．
故选C
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．