Question

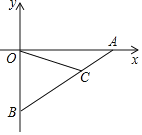
【题目】如图所示，直线AB交x轴于点A（，0），交y轴于点B（0，），且．b满足

（1）求证：OA=OB；

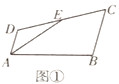
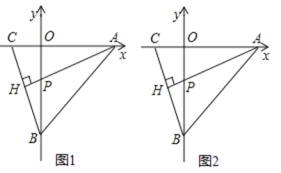
（2）如图1，若C的坐标为（-1，0），且AH⊥BC于点H，AH交OB于点P，试求点P的坐标；

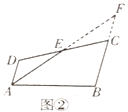
（3）如图2，连接OH，求证：∠OHP=45°．

Answer 1

【答案】（1）详见解析；（2）点P坐标为（0，-1）；（3）详见解析．

【解析】

（1）通过非负性先求出a和b的值，进而即可得解；

（2）通过证明，得到OP=OC=1，进而即可得解；

（3）过点O分别作OM⊥CB于点M，作ON⊥HA于点N，通过证明，进行求解即可.

（1）证明：∵，且，

∴，

∴，

∴OA=OB=4；

（2）解：∵AH⊥BC于H，

∴∠OAP+∠OPA=∠BPH+∠OBC=90°，

∵∠OPA=∠BPH

∴∠OAP=∠OBC

∵∠COB＝∠POA＝90°，OA＝OB

∴

∴OP=OC=1

∴点P坐标为；

（3）解：如下图，过点O分别作OM⊥CB于点M，作ON⊥HA于点N，连接OH．

∴

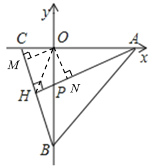
∵∠OAP=∠OBC，OB=OA

∴

∴OM=ON

∵OH=OH

∴

∴∠OHM=∠OHN

∵

∴.