题目内容
【题目】在数学活动课上,数学老师出示了如下题目:
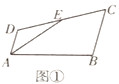
如图①,在四边形![]() 中,
中,![]() 是边
是边![]() 的中点,
的中点,![]() 是
是![]() 的平分线,
的平分线,![]() .
.
求证:![]() .
.
小聪同学发现以下两种方法:
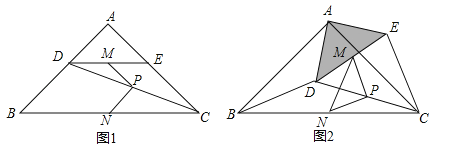
方法1:如图②,延长![]() 、
、![]() 交于点
交于点![]() .
.
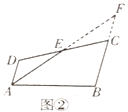
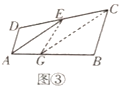
方法2:如图③,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() .
.
(1)请你任选一种方法写出这道题的完整的证明过程;
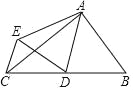
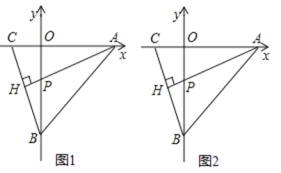
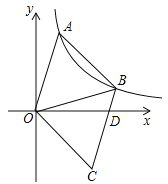
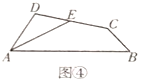
(2)如图④,在四边形![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)方法1:证明见解析;方法2:证明见解析;(2)证明见解析.
【解析】
(1)方法1:先根据角平分线的定义、平行线的性质得出![]() ,再根据等腰三角形的性质可得
,再根据等腰三角形的性质可得![]() ,根据三角形全等的判定定理与性质得出
,根据三角形全等的判定定理与性质得出![]() ,然后根据线段的和差即可得证;
,然后根据线段的和差即可得证;
方法2:先根据角平分线的定义得出![]() ,再根据三角形全等的判定定理与性质可得
,再根据三角形全等的判定定理与性质可得![]() ,然后根据线段中点的定义、等腰三角形的性质可得
,然后根据线段中点的定义、等腰三角形的性质可得![]() ,最后根据平行线的性质、平角的定义可得
,最后根据平行线的性质、平角的定义可得![]() ,由等腰三角形的定义可得
,由等腰三角形的定义可得![]() ,由此根据线段的和差即可得证;
,由此根据线段的和差即可得证;
(2)如图(见解析),参照方法1构造辅助线,先根据等腰三角形的性质得出![]() 平分
平分![]() ,从而有
,从而有![]() ,再根据平行线的性质、角的和差得出
,再根据平行线的性质、角的和差得出![]() ,
,![]() ,然后根据三角形全等的判定定理与性质即可得证.
,然后根据三角形全等的判定定理与性质即可得证.
(1)方法1:如图②,延长![]() 、
、![]() 交于点
交于点![]()
![]() 是
是![]() 的平分线
的平分线
![]()
![]()
![]()
![]()
![]()
![]()
![]() 是边
是边![]() 的中点
的中点
![]()
在![]() 和
和![]() 中,
中,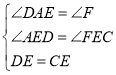
![]()
![]()
![]() ;
;
方法2:如图③,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]()
![]() 是
是![]() 的平分线
的平分线
![]()
在![]() 和
和![]() 中,
中,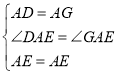
![]()
![]()
![]()
![]() 是边
是边![]() 的中点
的中点
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
又![]()
![]()
![]()
![]() ;
;
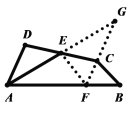
(2)如图,过点C作![]() ,交AE延长线于点G,延长GC交AB于点F,连接EF
,交AE延长线于点G,延长GC交AB于点F,连接EF
由方法1可知:![]()
![]() 是等腰三角形
是等腰三角形
![]() 平分
平分![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]()
在![]() 和
和![]() 中,
中,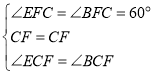
![]()
![]() .
.

练习册系列答案
相关题目