题目内容
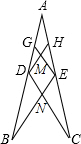
 如图,已知AB=AC,D、E分别为AB、AC的中点,G、H分别为AD、AE的中点,则图中的全等三角形共有( )
如图,已知AB=AC,D、E分别为AB、AC的中点,G、H分别为AD、AE的中点,则图中的全等三角形共有( )分析:根据题意,结合图形,可得知△ADH≌△AEG,△GDM≌△HEM,△ABE≌△ACD,△GEB≌△HDC,△DBN≌△ECN,做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.
解答:解:∵AB=AC,D、E分别为AB、AC的中点,G、H分别为AD、AE的中点,
 ∴AD=AE=DB=EC,AG=AH=GD=HE,
∴AD=AE=DB=EC,AG=AH=GD=HE,
∴GB=HC,
①△ABE≌△ACD,
∵
,
∴△ABE≌△ACD(SAS),
∴∠B=∠C,BE=CD,
②△DBN≌△ECN,
∵
,
∴△DBN≌△ECN(AAS),
③△GEB≌△HDC,
∵
,
∴△GEB≌△HDC(SAS),
∴GE=HD,
③△ADH≌△AEG,
∵
,
∴△ADH≌△AEG(SSS),
∴∠ADH=∠AEG,
⑤△GDM≌△HEM,
∵
,
∴△GDM≌△HEM(AAS).
共5对.
故选C.
 ∴AD=AE=DB=EC,AG=AH=GD=HE,
∴AD=AE=DB=EC,AG=AH=GD=HE,∴GB=HC,
①△ABE≌△ACD,
∵
|
∴△ABE≌△ACD(SAS),
∴∠B=∠C,BE=CD,
②△DBN≌△ECN,
∵
|
∴△DBN≌△ECN(AAS),
③△GEB≌△HDC,
∵
|
∴△GEB≌△HDC(SAS),
∴GE=HD,
③△ADH≌△AEG,
∵
|
∴△ADH≌△AEG(SSS),
∴∠ADH=∠AEG,
⑤△GDM≌△HEM,
∵
|
∴△GDM≌△HEM(AAS).
共5对.
故选C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )
如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )| A、60° | B、90° | C、45° | D、120° |
 10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( )
10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( ) 26、如图,已知AB=AC,AD=AE.求证BD=CE.
26、如图,已知AB=AC,AD=AE.求证BD=CE. 2、如图,已知AB=AC,AD=AE,BD=EC,则图中有
2、如图,已知AB=AC,AD=AE,BD=EC,则图中有 如图,已知AB=AC,BC=CD=AD,求∠B的值.
如图,已知AB=AC,BC=CD=AD,求∠B的值.