题目内容
【题目】数学实践活动课中小明同学测量某建筑物
的高度，如图，已知斜坡
的坡度为
，小明在坡底点
处测得建筑物顶端
处的仰角为
，他沿着斜坡行走
米到达点
处，在测得建筑 物顶端处的仰角为
，小明和建筑物的剖面在同一平面内，小明的身高忽略不计．则建筑物的高度约为（ ）（参考数据：
）
A.
米B.
米C.
米D.
米
【答案】D
【解析】
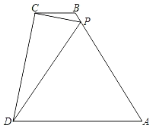
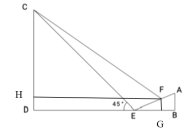
如图，过F点作FH⊥CD，垂足为H，作FG⊥EB，垂足为G.利用坡度先求出FG与EG，设DE=CD=x，表示出FH，CH，再利用三角函数即可解得.
如图，过F点作FH⊥CD，垂足为H，作FG⊥EB，垂足为G.
根据题意易知DC=DE，EF=13m，∠CFH=35°，HF=GD，HD=FG
∵斜坡
的坡度为
，且EF=13m
故FG=5m，EG=12m
设DE=CD=x，则FH=DE+EG=x+12，CH=CD-HD=CD-FG=x-5
在直角三角形CHF中，
解得x≈44.7
故选D
练习册系列答案
相关题目
【题目】数学学习小组根据函数学习的经验，对一个新函数
的图象和性质进行了如下探究：
列表，下表是函数
与自变量
的几组对应值
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
请直接写出
如图，在平面直角系
中，描出上表中各对对应值为坐标的点 （其中为横坐标，为纵坐标），并根据描出的点画出函数的图象
观察所画出的函数图象，写出该函数的性质（写一条性质即可）
请结合画出的函数图象与表格中数据，直接写出关于的不等式的解集：
