Question

【题目】已知AB为⊙O的直径，点C为⊙O上一点，点D为AB延长线一点，连接AC．

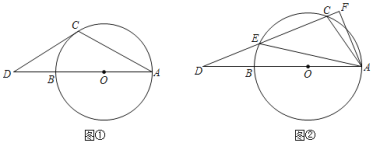
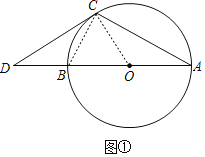
(Ⅰ)如图①，OB=BD，若DC与⊙O相切，求∠D和∠A的大小；

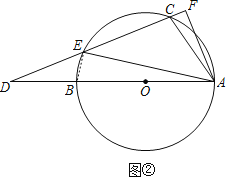
(Ⅱ)如图②，CD与⊙O交于点E，AF⊥CD于点F连接AE，若∠EAB=18°，求∠FAC的大小．

Answer 1

【答案】(Ⅰ)∠D=∠A=30°；(Ⅱ)18°

【解析】

(Ⅰ)如图①，连接OC，BC，根据已知条件可以证明△OBC是等边三角形，进而可得∠D和∠A的大小；

(Ⅱ)如图②，连接BE，根据AB为⊙O的直径，可得∠AEB=90°，由AF⊥CD，得∠AFC=90°，再根据∠ACF是圆内接四边形ACEB的外角，即可求∠FAC的大小．

(Ⅰ)如图①，连接OC，BC，

∵AB为⊙O的直径，

∴∠ACB=90°，

∵DC与⊙O相切，

∴∠OCD=90°，

∵OB=BD，

∴BC=OD=OB=BD，

∴BC=OB=OC，

∴△OBC是等边三角形，

∴∠OBC=∠OCB=∠COB=60°，

∴∠BCD=∠OCA=30°，

∴∠D=∠A=30°；

(Ⅱ)如图②，连接BE，

∵AB为⊙O的直径，

∴∠AEB=90°，

∵AF⊥CD，

∴∠AFC=90°，

∵∠ACF是圆内接四边形ACEB的外角，

∴∠ACF=∠ABE，

∴∠FAC=∠EAB=18°，

答：∠FAC的大小为18°．