题目内容
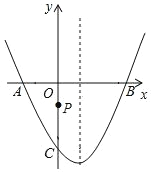
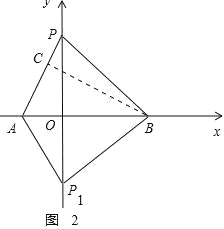
【题目】如图，在平面直角坐标系中，二次函数 y＝ax2+bx+c 的图象交 x 轴于A、B 两点，交 y 轴于 C 点，P 为 y 轴上的一个动点，已知 A（﹣2，0）、C（0，﹣2
），且抛物线的对称轴是直线 x＝1．
(1)求此二次函数的解析式；
(2)连接 PB，则 
PC+PB 的最小值是 ；
(3)连接 PA、PB，P 点运动到何处时，使得∠APB＝60°，请求出 P 点坐标．
【答案】（1）y＝
x2﹣
x﹣2 
；（2）3；（3）P（0，+
），（0，﹣﹣）．
【解析】
(1)根据待定系数法，可得答案；(2)连接 AC，作 BH⊥AC 于 H，交 OC 于 P，此时
PC+PB 最小．最小值就是线段 BH，求出 BH 即可．(3)根据勾股定理，可得 PA，PB，根据锐角三角函数，可得 BC 的长，根据三角形的面积，可得关于 n 的方程，根据解方程，可得答案．
（1）将 A，C 点坐标代入函数解析式，及对称轴，得
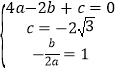解得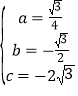
抛物线的解析式为 y＝x2﹣x﹣2 ，
(2)连接 AC，作 BH⊥AC 于 H，交 OC 于 P，如图 1，此时PC+PB 最小．
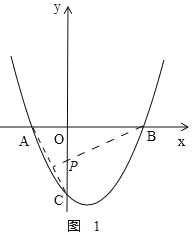
理由：当 y＝0 时，x2﹣x﹣2＝0，解得 x＝﹣2（舍）x＝4，即 B（4，0）， AB＝4﹣（﹣2）＝6．
∵OA＝2，OC＝2 ，
∴tan∠ACO＝ 
，
∴∠ACO＝30°，
∴PH＝PC，
∴PC+PB＝PH+PB＝BH，
∴此时PB+PD 最短（垂线段最短）．
在 Rt△ABH 中，∵∠AHB＝90°，AB＝4﹣（﹣2）＝6，∠HAB＝60°，
∴sin60°＝
＝，
∴BH＝6×＝3，
∴PC+PB 的最小值为 3， 故答案为：3．
(3)如图 2，作 BC⊥PA 于 C，设 P（0，n），由勾股定理，得 PB＝ 
，PA＝ 
，
由 sin∠APB＝sin60°，得∠CPB＝ 
，
∴BC＝
，
由 S△PAB＝AB|n|＝ APBC，得
6|n|＝ 
,
化简，得 n4﹣28n2+64＝0，
解得 n＝14+2
，n＝14﹣2 （不符合题意，舍）
＝ 
＝+，
＝﹣＝﹣﹣
∴P（0，+），（0，﹣﹣）．
