题目内容
【题目】已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为cm. 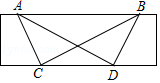
【答案】4 ![]()
【解析】解:设E为AB中点, ∵∠ACB=∠ADB=90°,
∴A,B,C,D在以AB为直径的圆上,
连接DE,CE,则CE=DE= ![]() AB=4,
AB=4,
作EF⊥CD交CD于F,
∴CD=2CF,
∵AB∥CD,
∴EF=2,
在Rt△CFE和Rt△DFE中,CF= ![]() =
= ![]() =2
=2 ![]() ,
,
∴CD=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目