题目内容
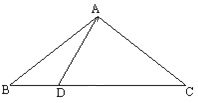
【题目】已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A。
求:BD的长。
【答案】![]()
【解析】
先根据等腰三角形的性质和勾股定理求出AE=6,设BD=x,则DE=8﹣x,DC=16﹣x.在Rt△ADE和Rt△ADC中利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,继而代入求出x的值即可.
如图,过点A作AE⊥BC于点E,
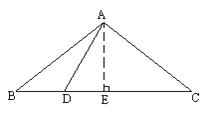
∵AB=AC=10,BC=16,∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE=![]() =
=![]() =6,
=6,
设BD=x,则DE=8﹣x,DC=16﹣x,
又DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2﹣AC2,
代入为:62+(8﹣x)2=(16﹣x)2﹣102,解得:x=![]() .
.
即BD=![]() .
.

练习册系列答案
相关题目