题目内容
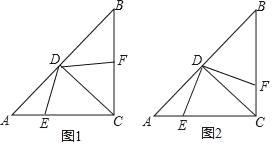
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E,F分别是边AC, BC上的动点,AC=4,设AE=x,BF=y.
(1)若x+y=3,求四边形CEDF的面积;
(2)当DE⊥DF时,如图2,试探索x、y之间的数量关系.
【答案】(1)S四边形CEDF= 5;(2)x+y=4.
【解析】
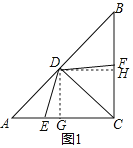
(1)在图1中,过点D作DG⊥AC于点G,DH⊥BC于点H,由∠ACB=90°、AC=BC、CD是∠ACB的角平分线可得出∠A=∠B=∠ACD=∠BCD=45°,进而可得出AD=CD=BD,根据等腰直角三角形的性质可求出DG=DH=2,利用三角形的面积结合S四边形CEDF=S△CDE+S△CDF、x+y=3,即可求出四边形CEDF的面积;
(2)由DE⊥DF、CD⊥AB可得出∠ADE=∠CDF,结合AD=CD、∠A=∠DCF=45°,即可证出△ADE≌△CDF(ASA),根据全等三角形的性质可得出AE=CF,进而可得出AE+BF=CF+BF=BC,即x+y=4.
(1)在图1中,过点D作DG⊥AC于点G,DH⊥BC于点H.
∵∠ACB=90°,AC=BC,CD是∠ACB的角平分线,
∴∠A=∠B=∠ACD=∠BCD=45°,
∴AD=CD=BD.
∵在等腰直角三角形ACD中,DG⊥AC,∠A=45°,
∴DG=AG=![]() AC=2,
AC=2,
同理:DH=2.
∵S△CDE=![]() CEDG=4-x,S△CDF=
CEDG=4-x,S△CDF=![]() CFDH=4-y,
CFDH=4-y,
∴S四边形CEDF=S△CDE+S△CDF=(4-x)+(4-y)=8-(x+y)=5;
(2)当DE⊥DF时,∠EDF=90°.
∵CD⊥AB,
∴∠ADE+∠EDC=∠EDC+∠CDF=90°,
∴∠ADE=∠CDF.
在△ADE与△CDF中,
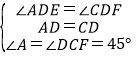 ,
,
∴△ADE≌△CDF(ASA),
∴AE=CF,
∴AE+BF=CF+BF=BC,即x+y=4.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案