题目内容
【题目】方程x2﹣kx+k﹣2＝0有两个实数根x1，x2，且0＜x1＜1，2＜x2＜3，求k的取值范围．
【答案】2＜k＜3.5．
【解析】
由于方程x2-kx+k-2=0有两个实数根x1，x2，且0＜x1＜1，2＜x2＜3，根据一元二次方程与二次函数的关系可画出二次函数y=x2-kx+k-2的图象，根据图象得到当x=0，y=k-2＞0；当x=1，y=1-k+k-2＜0；当x=2，y=4-2k+k-2＜0；当x=3，y=9-3k+k-2＞0，求出几个不等式解的公共部分即可得到k的取值范围．
∵方程x2-kx+k-2=0有两个实数根x1，x2，且0＜x1＜1，2＜x2＜3，
∴二次函数y=x2-kx+k-2如图所示，
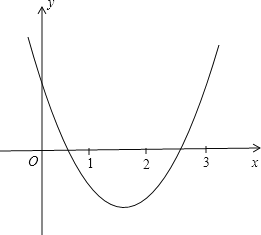
∴x=0，y=k-2＞0；x=1，y=1-k+k-2＜0；x=2，y=4-2k+k-2＜0；x=3，y=9-3k+k-2＞0，
而△=k2-4（k-2）=（k-2）2+4＞0，
∴2＜k＜3.5，
即k的取值范围为2＜k＜3.5．
练习册系列答案
相关题目
【题目】已知函数
（
为常数且
）中，当
时，
；当
时，
．请对该函数及其图像进行如下探究：
（1）求该函数的解析式，并直接写出该函数自变量
的取值范围：
（2）请在下列直角坐标系中画出该函数的图像：
列表如下：
x | … | -4 | -3 | -2 | -1 | 0 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | … |
描点连线：
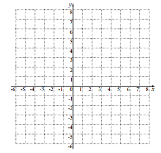
（3）请结合所画函数图象，写出函数图象的两条性质
（4）请你在上方直角坐标系中画出函数
的图像，结合上述函数的图像，写出不等式
的解集．