��Ŀ����
����Ŀ���Ķ�������ϣ����(1)-(3)�⣮
��ѧ���ϣ���ʦ��ʾ������һ���⣺
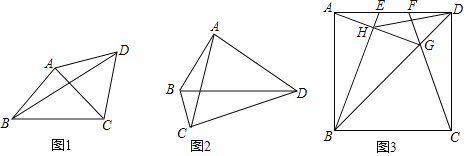
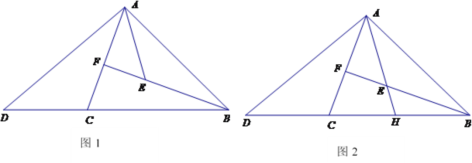
��ͼ1���ڡ�ABC�У�BA=BC��![]() ����F��AC�ϣ���E��BF�ϣ�
����F��AC�ϣ���E��BF�ϣ�![]() ����D��BC �ӳ����ϣ�����AD��AE����ACD+��DAE=180�b��̽���߶�AD��AE��������ϵ��֤����
����D��BC �ӳ����ϣ�����AD��AE����ACD+��DAE=180�b��̽���߶�AD��AE��������ϵ��֤����
ͬѧ�Ǿ���˼�����������ѵ��뷨��
С������ͨ���۲�Ͷ��������֡�CAD���EAB��ȣ���
С������ͨ���۲�Ͷ��������֡�FAE���DҲ��ȣ���
Сΰ����ͨ���߽ǹ�ϵ���츨���ߣ�������һ�����������Եõ��߶�AD��AE��������ϵ����
![]()
��ʦ��������ԭ���������ӳ�ͼ1�е�AE����BC�ཻ�ڵ�H(��ͼ2)����֪��DH��AH��������ϵ���������![]() ��ֵ����
��ֵ����
��1����֤����CAD=��EAB��
��2����![]() ��ֵ���ú�k��ʽ�ӱ�ʾ����
��ֵ���ú�k��ʽ�ӱ�ʾ����
��3����ͼ2����![]() ����
����![]() ��ֵΪ________���ú�k��ʽ�ӱ�ʾ����
��ֵΪ________���ú�k��ʽ�ӱ�ʾ����
���𰸡���1������������2��![]() ����3��
����3��![]() ��
��
��������
��1������BA=BC�ó���BAC=��BCA���ٸ�����������Ǻ͵�֪ʶ���ACD+��DAE=180�b����ACD+��ACB=180�b�ó���DAC=��BAE��
��2������һ������C����ACM=��ABE����AD�ڵ�M��֤������AEB�ס�AMC���������Ʊȵó�![]() ��
��![]() ���ٸ���������֤��DCM�ס�AFE���������Ʊȵõ�
���ٸ���������֤��DCM�ס�AFE���������Ʊȵõ�![]() ��AD=AM+DM=
��AD=AM+DM=![]() ���������
���������
������������B��BN��AC��AE�ӳ����ڵ�N��֤����AFE�ס�NBE����ACD�ס�ABN���������Ʊ���⼴�ɣ�
��3������B��BN��AC��AE�ӳ����ڵ�N����֤��AHC��DHA���������Ʊȵõ�![]() ������
������![]() ��
��![]() ���ó�
���ó�![]() ����AH=2a��AB=BC=b��
����AH=2a��AB=BC=b��
����EH=AH-AE=EN-NH�����Ƶó�![]() ��
��![]() �����ɡ�ADH�ס�NBH��������������ó�
�����ɡ�ADH�ס�NBH��������������ó�![]() �����b���ɣ�
�����b���ɣ�
(1)��BA=BC��
���BAC=��BCA��
�ߡ�ACD+��DAE=180�b��
��ACD+��ACB=180�b��
���DAE=��ACB��
���DAE=��BAC��
���DAC=��BAE��
(2)����һ��
����C����ACM=��ABE����AD�ڵ�M��
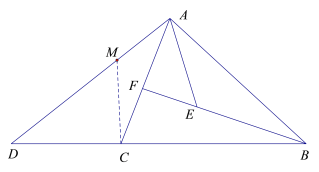
�ߡ�DAC=��BAE��
���AEB�ס�AMC��
��![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��
�ߡ�AEF=��EAB+��ABE��
��DMC=��MAC+��ACM��
���DMC=��AEF��
�ߡ�ACB=��D+��DAC��
��DAE=DAC+��FAE��
��DAE=��ACB��
���D=��FAE��
���DCM�ס�AFE��
��![]() ��
��
��![]() ��
��
��AD=AM+DM=![]() ��
��
��![]() ��
��
��������
����B��BN��AC��AE�ӳ����ڵ�N��
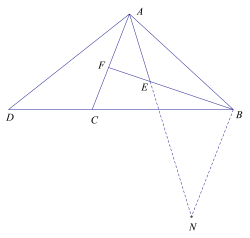
���N=��FAE��
��AFE=��EBN��
���AFE�ס�NBE��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ߡ�ACB=��D+��DAC��
��DAE=DAC+��FAE��
��DAE=��ACB��
���D=��FAE��
�ߡ�DAC=��BAE��
���ACD�ס�ABN��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��3��ͬ������������
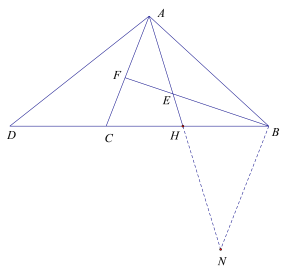
�ߡ�D=��CAH����AHC=��DHA��
���AHC��DHA��
��![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��AH=2a��AB=BC=b��
��DH=3a, ![]() ��
��
��NE=2AE��
��NE=b��
��EH=AH-AE=EN-NH��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���ɷ��������Ƶã�
![]() ��
��
�ߡ�ADH�ס�NBH��
��![]() ��
��
��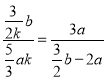 ��
��
��![]() ��
��
��![]() ���ᣩ��
���ᣩ�� ![]() ��
��
��![]() ��
��