题目内容
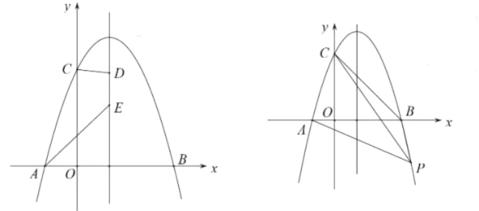
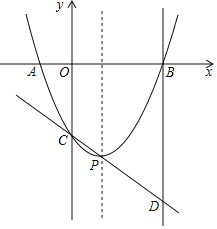
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,顶点为P,直线
轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,顶点为P,直线![]() 与过点B且垂直于
与过点B且垂直于![]() 轴的直线交于点D,且CP:PD=1:2,tan∠PDB=
轴的直线交于点D,且CP:PD=1:2,tan∠PDB=![]() .
.
(1)请直接写出A、B两点的坐标:A , B ;
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M使|MC-MB|的值最大,则点M的坐标为____.
【答案】(1)B(3,0),A(-1,0);(2)y=![]() ;(3)(1,-
;(3)(1,-![]() ).
).
【解析】
(1)先求得抛物线的对称轴为x=1,然后利用平行线分线段成比例定理求得OE:EB的值,从而得到点B的坐标,利用抛物线的对称性可求得点A的坐标;
(2)过点C作CF⊥PE,垂足为F.先求得点C和点P的坐标(用含字母的式子表示),然后可得到PF=a,然后利用锐角三角函数的定义可求得a的值,然后将点A和点B的坐标代入抛物线的解析式可求得c的值;
(3)根据三角形的任意两边之差小于第三边判断出点A、C、M在同一直线上时|MC-MB|最大,设直线AC的解析式为y=kx+b,利用待定系数法求出一次函数解析式,再根据点M在对称轴上代入计算即可得解.
解:(1)如图所示:
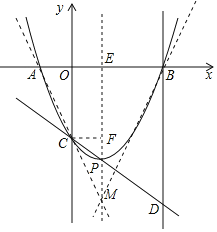
∵由题意可知:抛物线的对称轴为x=1,
∴OE=1.
∵OC∥PE∥BD,CP:PD=1:2,
∴![]() .
.
∴BE=2.
∴OB=3.
∴B(3,0).
∵点A与点B关于PE对称,
∴点A的坐标为(-1,0).
故答案是:-1,0;3,0;
(2)过点C作CF⊥PE,垂足为F.
将x=0代入得:y=c,
∴点C的坐标为(0,c).
将x=1代入得y=-a+c.
∴点P的坐标为(1,-a+c).
∴PF=a.
∵PE∥BD,tan∠PDB=![]() ,
,
∴tan∠CPF=tan∠PDB=![]() .
.
∴![]() .
.
解得a=![]() .
.
将a=![]() 代入抛物线的解析式得:y=
代入抛物线的解析式得:y=![]() x2-
x2-![]() x+c.
x+c.
将点A的坐标代入得:![]() +c=0,解得:c=-
+c=0,解得:c=-![]() .
.
∴抛物线的解析式为y=![]() .
.
(3)由三角形的三边关系,|MC-MB|<AC,
∴当点A、C、M在同一直线上时|MC-MB|最大,
设直线AC的解析式为y=kx+b,
则 ,
,
解得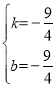 ,
,
∴y=-![]() x-
x-![]() ,
,
∵抛物线对称轴为直线x=1,
∴当x=1时,y=-![]() ×1-
×1-![]() =-
=-![]() ,
,
∴点M的坐标为(1,-![]() ).
).
故答案是:(1,-![]() ).
).