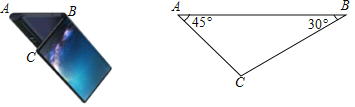题目内容
【题目】如图1是某小区入口实景图,图2是该入口抽象成的平面示意图,已知入口BC宽3.9米,门卫室外墙上的O点处装有一盏灯,点O与地面BC的距离为3.3米,灯臂OM长1.2米,(灯罩长度忽略不计),∠AOM=60°.

(1)求点M到地面的距离,
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车能否从该入口安全通过?如果能安全通过,请直接写出货车离门卫室外墙AB的最小距离(精确到0.01米);如果不能安全通过,请说明理由.(参考数据:![]() 1.73)
1.73)
【答案】(1)3.9米;(2)能,0.35米
【解析】
(1)可以过点M作MN⊥OA于点N,根据OM长1.2米,∠AOM=60°.得到ON=0.6米,进而可求得点M到地面的距离;
(2)过点A作AE⊥BA,垂足为A,设货车高AB=3.5米,进而求出AE的长即可说明.
如图所示,
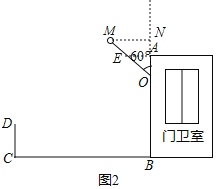
(1)过点M作MN⊥OA于点N,
∵OM长1.2米,∠AOM=60°.
∴ON=0.6米,
∴BN=OB+ON=3.3+0.6=3.9米.
答:点M到地面的距离为3.9米.
(2)一辆总宽2.55米,总高3.5米的货车能从该入口安全通过,理由如下:
过点A作AE⊥BA,垂足为A,
∵该货车高AB=3.5米,
则OA=3.5﹣3.3=0.2
∴AE=OAtan60°=0.2![]() ≈0.35(米)
≈0.35(米)
答:货车离门卫室外墙AB的最小距离为0.35米.

练习册系列答案
相关题目