题目内容
【题目】(操作思考)画⊙![]() 和⊙
和⊙![]() 的直径
的直径![]() 、弦
、弦![]() ,使
,使![]() ,垂足为
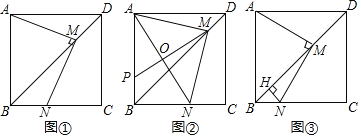
,垂足为![]() (如图1).猜想所画的图中有哪些相等的线段、相等的劣弧?(
(如图1).猜想所画的图中有哪些相等的线段、相等的劣弧?(![]() 除外).
除外).
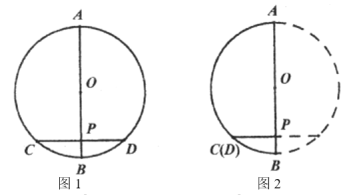
(1)猜想:① ;② ;③ .
操作:将图1中的![]() 沿着直径
沿着直径![]() 翻折,因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,所以
翻折,因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,所以![]() 与
与![]() 重合,又因为
重合,又因为![]() ,所以射线
,所以射线![]() 与射线
与射线![]() 重合(如图2),于是点
重合(如图2),于是点![]() 与点
与点![]() 重合,从而证实猜想.
重合,从而证实猜想.
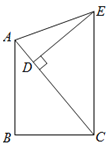
(知识应用)图3是某品牌的香水瓶,从正面看上去(如图4),它可以近似看作割去两个弓形后余下的部分与矩形![]() 组合而成的图形(点
组合而成的图形(点![]() 在
在![]() 上),其中
上),其中![]() .
.
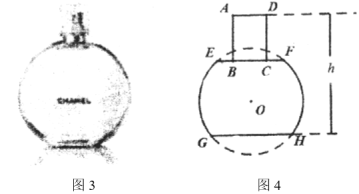
(2)已知⊙![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() ,
,![]() ,求香水瓶的高度
,求香水瓶的高度![]() .
.
【答案】(1)CP=DP,![]() ,
,![]() ;(2)7.2cm
;(2)7.2cm
【解析】
(1)根据轴对称图形的定义及垂径定理即可得到答案;
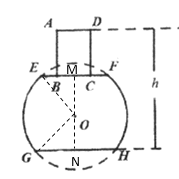
(2)作OM⊥EF,延长MO角GH于N,连接OE、OG,根据垂径定理分别求出EM、GN,利用勾股定理求出OM、ON,即可得到答案.
(1)∵⊙![]() 的直径
的直径![]() 、弦
、弦![]() ,使
,使![]() ,垂足为
,垂足为![]() ,
,
∴相等的线段是:CP=DP,相等的劣弧是:![]() ,
,![]() ,
,
故答案为:CP=DP,![]() ,
,![]() ;
;
(2)作OM⊥EF,延长MO角GH于N,连接OE、OG,
∵![]() ,
,
∴ON⊥GH,
∵EM=![]() EF=1.8cm,GN=
EF=1.8cm,GN=![]() GH=2.4cm,⊙
GH=2.4cm,⊙![]() 的半径为3cm,
的半径为3cm,
∴![]() ,
,![]() ,
,
∴香水瓶的高度![]() =AB+OM+ON=3+2.4+1.8=7.2cm.
=AB+OM+ON=3+2.4+1.8=7.2cm.

练习册系列答案
相关题目