题目内容
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足△BCP的周长为14cm,求此时t的值;
(2)若点P在∠BAC的平分线上,求此时t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)t为
;(3)t为![]() s或5.3s或5s或
s或5.3s或5s或![]() s时,△BCP为等腰三角形.
s时,△BCP为等腰三角形.
【解析】
(1)根据△BCP的周长为14cm, 可得AP=4t,PC=8-4t,BP=14-PC-BC=4t,根据勾股定理列出方程可求得t的值;
(2)过P作PE⊥AB,设CP=x,根据角平分线的性质和勾股定理列方程式求出CP,由此可求出t;
(3)分类讨论:当CP=CB时,△BCP为等腰三角形,若点P在AC上,根据AP的长即可得到t的值,若点P在AB上,根据P移动的路程易得t的值;当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,根据等腰三角形的性质得BD=CD,则可判断PD为△ABC的中位线,则AP=0.5AB=5,易得t的值;当BP=BC=6时,△BCP为等腰三角形,易得t的值.
(1)∵△ABC中,∠ACB=90°,AB=10cm,BC=6cm,
∴由勾股定理得![]() ,
,
如图,连接BP,
当△BCP的周长为14cm 时,
![]()
在![]() 中根据勾股定理
中根据勾股定理
![]()
即![]()
解得![]() .
.
故此时![]()
![]() ;
;
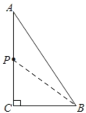
(2)如图1,过P作PE⊥AB,
又∵点P恰好在∠BAC的角平分线上,且∠C=90°,AB=10cm,BC=6cm,
∴CP=EP,
∴△ACP≌△AEP(HL),
∴AC=8cm=AE,BE=2,
设CP=x,则BP=6x,PE=x,
∴Rt△BEP中,BE2+PE2=BP2,
即22+
解得x=![]() ,
,
∴CP=![]() ,
,
∴CA+CP=8+![]() =
=![]() ,
,
∴![]() ;
;
(3)①如图2,当CP=CB时,△BCP为等腰三角形
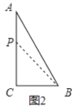
若点P在CA上,则4t=86,
解得t=![]() (s);
(s);
②如图3,
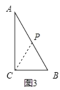
当BP=BC=6时,△BCP为等腰三角形,
∴AC+CB+BP=8+6+6=20,
∴t=20÷4=5(s);
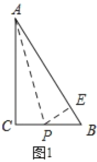
③如图4,
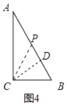
若点P在AB上,CP=CB=6,作CD⊥AB于D,则根据面积法求得CD=4.8,
在Rt△BCD中,由勾股定理得,BD=3.6,
∴PB=2BD=7.2,
∴CA+CB+BP=8+6+7.2=21.2,
此时t=21.2÷4=5.3(s);
④如图5,
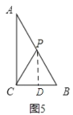
当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,则D为BC的中点,
∴PD为△ABC的中位线,
∴AP=BP=![]() AB=5,
AB=5,
∴AC+CB+BP=8+6+5=19,
∴t=19÷4=![]() (s);
(s);
综上所述,t为![]() s或5.3s或5s或
s或5.3s或5s或![]() s时,△BCP为等腰三角形.
s时,△BCP为等腰三角形.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案