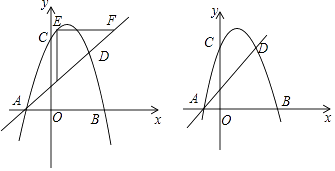题目内容
【题目】如图,已知![]() 中,
中, ![]() ,
, ![]() ,
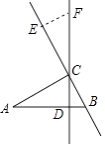
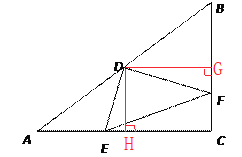
, ![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作![]() 交BC边于点F,联结EF.
交BC边于点F,联结EF.
(1)如图1,当![]() 时,求EF的长;
时,求EF的长;
(2)如图2,当点E在AC边上移动时, ![]() 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出![]() 的正切值;
的正切值;
(3)如图3,联结CD交EF于点Q,当![]() 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.

【答案】(1)![]() ;(2)不变;(3)
;(2)不变;(3)![]() 或3或
或3或![]() .
.
【解析】试题分析:(1)由已知条件易求DE=3,DF=4,再由勾股定理EF=5;
(2)过点![]() 作
作![]() ,
, ![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,由(1)可得DH=3,DG=4;再证
,由(1)可得DH=3,DG=4;再证![]() ,即可得出结论;
,即可得出结论;
(3)分三种情况讨论即可.
(1)∵![]() ,
, ![]()
∴![]()
∵![]()
∴![]()
∵![]() 是
是![]() 边的中点
边的中点
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵在![]() 中,
中, ![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴四边形![]() 是矩形
是矩形
∴![]()
∵在![]() 中,
中, ![]()
∴![]()
(2)不变
过点![]() 作
作![]() ,
, ![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]()
由(1)可得![]() ,
, ![]()
∵![]() ,
, ![]()
∴![]()
又∵![]() ,
,
∴四边形![]() 是矩形
是矩形
∴![]()
∵![]()
∴![]() 即
即![]()
又∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
(3)1° 当![]() 时,易证
时,易证![]() ,即
,即![]()
又∵![]() ,D是AB的中点
,D是AB的中点
∴![]()
∴![]()
2° 当![]() 时,易证
时,易证![]()
∵在![]() 中,
中, ![]()
∴设![]() ,则
,则![]() ,
, ![]()
当![]() 时,易证
时,易证![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴
∴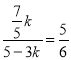 解得
解得![]()
∴![]()
∴![]()
3° 在BC边上截取BK=BD=5,由勾股定理得出![]()
当![]() 时,易证
时,易证![]()
∴设![]() ,则
,则![]() ,
, ![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴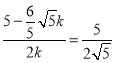 解得
解得![]()
∴![]()
∴![]()

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目