题目内容
【题目】在平行四边形ABCD中,![]() ,
,![]() ,
,![]() 绕点C旋转,角的两边分别与AB、AD交于点E、F,同时也分别与DA、BA的延长线交于点G、H.
绕点C旋转,角的两边分别与AB、AD交于点E、F,同时也分别与DA、BA的延长线交于点G、H.
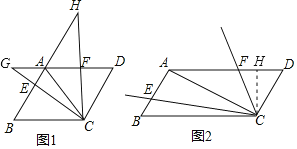
![]() 如图1,若
如图1,若![]() .
.
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 在
在![]() 绕点C旋转的过程中,线段AC、AG、AH之间存在着怎样的数量关系?并说明理由.
绕点C旋转的过程中,线段AC、AG、AH之间存在着怎样的数量关系?并说明理由.
![]() 如图2,若
如图2,若![]() ,经探究得
,经探究得![]() 的值为常数k,求k的值.
的值为常数k,求k的值.

【答案】![]() 证明见解析;
证明见解析;![]() ,理由见解析;
,理由见解析;![]() .
.
【解析】
![]() 如图
如图![]() 先证明四边形
先证明四边形![]() 为菱形,再证明
为菱形,再证明![]() ,
,![]() ,
,![]() ,根据ASA即可证明
,根据ASA即可证明![]() ≌
≌![]() ;
;
![]() 先证明
先证明![]() ,
,![]() ,根据两角对应相等的两三角形相似得出
,根据两角对应相等的两三角形相似得出![]() ∽
∽![]() ,利用相似三角形对应边成比例得出
,利用相似三角形对应边成比例得出![]() ;
;
![]() 如图2,过点
如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() 根据平行四边形的性质求出
根据平行四边形的性质求出![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 在直角
在直角![]() 中根据勾股定理求出
中根据勾股定理求出![]() ,由
,由![]() ,利用勾股定理的逆定理得出
,利用勾股定理的逆定理得出![]() ,再根据四边形内角和定理以及邻补角定义得出
,再根据四边形内角和定理以及邻补角定义得出![]() ,而
,而![]() ,那么
,那么![]() ∽
∽![]() ,
,![]() ,在直角
,在直角![]() 中由
中由![]() 得出
得出![]() ,即
,即![]() ,代入
,代入![]() ,即可求出
,即可求出![]() .
.
![]() 证明:如图1.
证明:如图1.
![]() 四边形ABCD为平行四边形,且
四边形ABCD为平行四边形,且![]() ,
,
![]() 四边形ABCD为菱形.
四边形ABCD为菱形.
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ;
;
![]() 解:如图1,
解:如图1,![]() ,理由如下:
,理由如下:
![]() 四边形ABCD为菱形,且
四边形ABCD为菱形,且![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ;
;
![]() 解:如图2,过点C作
解:如图2,过点C作![]() ,垂足为H.
,垂足为H.
![]() 四边形ABCD为平行四边形,
四边形ABCD为平行四边形,![]() ,
,
![]() .
.
设![]() ,则有
,则有![]() ,
,![]()
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在四边形AECF中,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目





