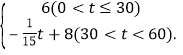��Ŀ����
����Ŀ��ij��˾�ɳ��׳�ǰ��ij���������ʱ����һ���������ͳ�����ͬʱ����������ͬһ����·��������ʻ���ٶȱ��ֲ��䣩��Ϊ��ȷ��������λ�ã�������OX��ʾ������·��ԭ��OΪ��ǧ��·�꣬��������Լ�����ٶ�Ϊ������ʾ�������������������ʻ���ٶ�Ϊ������ʾ����������ĸ�������ʻ���ٶ�Ϊ�㣬��ʾ������ֹ���г�Ϊ������ʾ����λ����ǧ���Ҳࣻ�г�Ϊ������ʾ����λ����ǧ����ࣻ�г�Ϊ�㣬��ʾ����λ����ǧ�״��������г̼�¼�����

����������е����ݣ�����������⣺
��1���׳�����7Сʱʱ��λ��Ϊ�� ��km���������ͳ�����λ��Ϊ�� ��km��
��2��������ͬʱ����xСʱʱ���׳�λ��Ϊ�� ��km���������ͳ�λ��Ϊ�� �� km ����x�Ĵ���ʽ��ʾ����
��3���׳�����ǰ����δ���ͣ�����������˾���ŷ������������ͽ�����ʻ3Сʱ���ʣ��׳�������ʻ3Сʱ���ܷ����̻���������ͳ��İ�������˵�����ɣ�
���𰸡���1����90����80��
��2��190��40x����80+50x��
��3���׳������̻���������ͳ��İ�����
�������������������1�����ݼ׳���λ�ú�ʱ������׳����ٶȣ�����ԭ����λ�ü�ȥ7Сʱ�Ժ��λ�ã���������׳�����7Сʱʱ��λ�ã�����5Сʱ��������λ�ú�7Сʱ��λ��������������ٶȣ��ٸ���·��=�ٶȡ�ʱ�䣬���ɵó��𰸣���2�����ݣ�1��������ٶȵó�xСʱ���·�̣�����ԭλ�ü�ȥ���ڵ�λ�ü��ɵó��׳���λ�ã��ã�1��������������ٶȳ���ʱ��������ڵ�λ�ã��ټ���������ԭ����λ�ü��ɵó��𰸣���3���ȼ��������3Сʱ�׳���λ�ú��������ͳ���λ�ã����߱Ƚϼ��ɵó��𰸣�
���������
��1����������ã�
�׳�����7Сʱʱ��λ��Ϊ��190-7����200��5��=-90��km����
�������ͳ�����λ��Ϊ��270-��270-170����2��7=-80��km����
�ʴ�Ϊ����90����80��
��2����������ã�
������ͬʱ����xСʱʱ���׳�λ��Ϊ��190��40x��
�������ͳ�λ��Ϊ����80+50x��
��3����x=3ʱ���׳�������λ���ǣ�190��40x=70��km����
�������ͳ���λ���ǣ���80+50x=70��km����
��׳������̻���������ͳ��İ�����