题目内容
如图,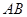 是
是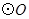 的直径,弦
的直径,弦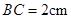 ,
,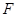 是弦
是弦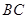 的中点,
的中点,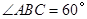 .若动点
.若动点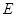 以
以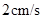 的速度从
的速度从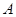 点出发沿着
点出发沿着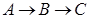 方向运动,设运动时间为
方向运动,设运动时间为 ,连结
,连结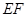 ,当
,当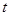 值为
值为 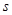 时,
时,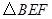 是直角三角形.
是直角三角形.
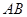 是
是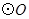 的直径,弦
的直径,弦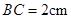 ,
,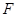 是弦
是弦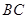 的中点,
的中点,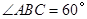 .若动点
.若动点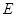 以
以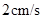 的速度从
的速度从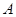 点出发沿着
点出发沿着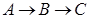 方向运动,设运动时间为
方向运动,设运动时间为 ,连结
,连结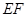 ,当
,当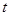 值为
值为 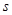 时,
时,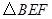 是直角三角形.
是直角三角形.
1或1.75或2.25s
若△BEF是直角三角形,则有两种情况:①∠BFE=90°,②∠BEF=90°;在上述两种情况所得到的直角三角形中,已知了BC边和∠B的度数,即可求得BE的长;AB的长易求得,由AE=AB-BE即可求出AE的长,也就能得出E点运动的距离(有两种情况),根据时间=路程÷速度即可求得t的值.
解:∵AB是⊙O的直径,
∴∠ACB=90°;
Rt△ABC中,BC=2,∠ABC=60°;
∴AB=2BC=4cm;
①当∠BFE=90°时;
∵Rt△BEF中,∠ABC=60°,BC=2cm,
∴AB=2BC=4cm,
∵F是弦BC的中点,
∴当△BEF是直角三角形时点E与点O重合,
∴BE=2BF=2cm;
故此时AE=AB-BE=2cm;
∴E点运动的距离为:2cm或6cm,故t=1s或3s;
由于0≤t<3,故t=3s不合题意,舍去;
所以当∠BFE=90°时,t=1s;
②当∠BEF=90°时;
同①可求得BE= BF=0.5cm,此时BE=AB-AE=3.5cm;
BF=0.5cm,此时BE=AB-AE=3.5cm;
∴E点运动的距离为:3.5cm或4.5cm,故t=1.75s或2.25s;
综上所述,当t的值为1、1.75或2.25s时,△BEF是直角三角形.
此题主要考查了圆周角定理以及直角三角形的判定和性质,同时还考查了分类讨论的数学思想.
解:∵AB是⊙O的直径,
∴∠ACB=90°;
Rt△ABC中,BC=2,∠ABC=60°;
∴AB=2BC=4cm;
①当∠BFE=90°时;
∵Rt△BEF中,∠ABC=60°,BC=2cm,
∴AB=2BC=4cm,
∵F是弦BC的中点,
∴当△BEF是直角三角形时点E与点O重合,
∴BE=2BF=2cm;
故此时AE=AB-BE=2cm;
∴E点运动的距离为:2cm或6cm,故t=1s或3s;
由于0≤t<3,故t=3s不合题意,舍去;
所以当∠BFE=90°时,t=1s;
②当∠BEF=90°时;
同①可求得BE=
 BF=0.5cm,此时BE=AB-AE=3.5cm;
BF=0.5cm,此时BE=AB-AE=3.5cm;∴E点运动的距离为:3.5cm或4.5cm,故t=1.75s或2.25s;
综上所述,当t的值为1、1.75或2.25s时,△BEF是直角三角形.
此题主要考查了圆周角定理以及直角三角形的判定和性质,同时还考查了分类讨论的数学思想.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目

 ⊙O相切,求t的值.
⊙O相切,求t的值.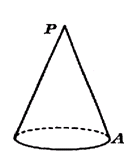

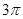 cm2,则扇形的圆心角是 ▲_ °,扇形的弧
cm2,则扇形的圆心角是 ▲_ °,扇形的弧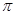 )
)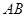 是 mm
是 mm