题目内容
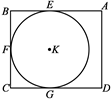
定义:一个定点与圆上各点之间距离的最小值称为这个点与这个圆之间的距离.现有一矩形ABCD如图所示,AB=14cm,BC=12cm,⊙K与矩形的
边AB、BC、CD分别相切于点E、F、G,则点A与⊙K的距离为_______cm.
边AB、BC、CD分别相切于点E、F、G,则点A与⊙K的距离为_______cm.
 |
4
分析:连KE,KF,连AK交⊙K于M点,根据切线的性质得KE⊥AB,KG⊥CD,KF⊥BC,则点E、K、G共线,四边形BCGE为矩形,四边形BFKE为正方形,BE=EK=KF=6cm,在Rt△PEK中利用勾股定理可求出AK,则可得到AM的长,然后根据点与圆之间的距离的定义即可得到点A与⊙K的距离.
解答:解:连KE,KG ,KF,连AK交⊙K于M点,如图,
,KF,连AK交⊙K于M点,如图,
∵AB、CD、BC与⊙K相切,
∴KE⊥AB,KG⊥CD,KF⊥BC,
而AB∥CD,
∴点E、K、G共线,
∴EG=BC=12cm,
∴EK=KF=6cm,
∴BE=6cm,
∴AE=AB-BE=14-6=8(cm),
在Rt△PEK中,AK2=AE2+KE2,
∴AK= =10,
=10,
∴AM=10-6=4(cm),
∴点A与⊙K的距离为4cm.
故答案为4.
解答:解:连KE,KG
 ,KF,连AK交⊙K于M点,如图,
,KF,连AK交⊙K于M点,如图,∵AB、CD、BC与⊙K相切,
∴KE⊥AB,KG⊥CD,KF⊥BC,
而AB∥CD,
∴点E、K、G共线,
∴EG=BC=12cm,
∴EK=KF=6cm,
∴BE=6cm,
∴AE=AB-BE=14-6=8(cm),
在Rt△PEK中,AK2=AE2+KE2,
∴AK=
 =10,
=10,∴AM=10-6=4(cm),
∴点A与⊙K的距离为4cm.
故答案为4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.
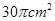 的扇形
的扇形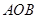 ,半径
,半径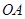 与地面垂直,在没有滑动的情况下,将扇形向右滚动至
与地面垂直,在没有滑动的情况下,将扇形向右滚动至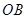 与地面垂直为止,则O点移动的距离为( )
与地面垂直为止,则O点移动的距离为( )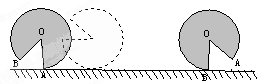
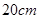
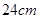
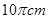
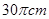
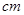 ,
,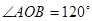 ,求
,求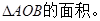

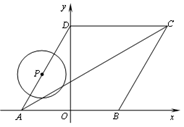
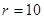 cm,圆心到直线
cm,圆心到直线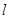 的距离OM=8cm,在直线
的距离OM=8cm,在直线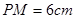 ,则点p( ).
,则点p( ).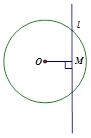
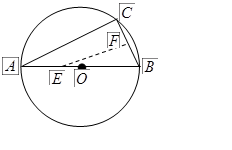
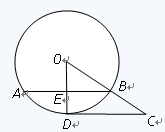
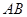 是
是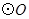 的直径,弦
的直径,弦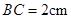 ,
,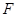 是弦
是弦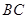 的中点,
的中点,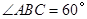 .若动点
.若动点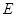 以
以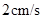 的速度从
的速度从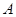 点出发沿着
点出发沿着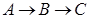 方向运动,设运动时间为
方向运动,设运动时间为 ,连结
,连结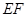 ,当
,当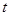 值为
值为 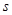 时,
时,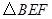 是直角三角形.
是直角三角形.