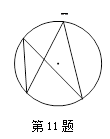
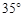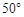题目内容
如图,底面半径为1,母线长为4的圆锥,一只小蚂蚁若从A点出发,绕侧面一周又回到A点,它爬行的最短路线长是___________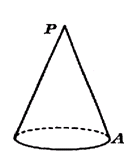

4
要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:由题意知,底面圆的直径为2,

故底面周长等于2π.
设圆锥的侧面展开后的扇形圆心角为n°,
根据底面周长等于展开后扇形的弧长得,2π= ,
,
解得n=90°,
所以展开图中圆心角为90°,
根据勾股定理求得到点A的最短的路线长是: .
.
解答:解:由题意知,底面圆的直径为2,

故底面周长等于2π.
设圆锥的侧面展开后的扇形圆心角为n°,
根据底面周长等于展开后扇形的弧长得,2π=
 ,
,解得n=90°,
所以展开图中圆心角为90°,
根据勾股定理求得到点A的最短的路线长是:
 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
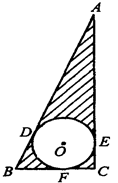
 是
是 的直径,弦
的直径,弦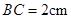 ,
,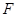 是弦
是弦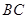 的中点,
的中点,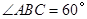 .若动点
.若动点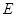 以
以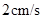 的速度从
的速度从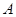 点出发沿着
点出发沿着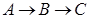 方向运动,设运动时间为
方向运动,设运动时间为 ,连结
,连结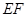 ,当
,当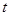 值为
值为 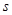 时,
时,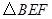 是直角三角形.
是直角三角形.
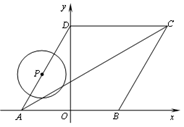
 与
与 轴相切于点
轴相切于点 ,与
,与 轴相交于点
轴相交于点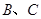 两点,连结
两点,连结 。
。

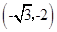 ,直接写出点
,直接写出点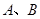 两点作⊙
两点作⊙ 与
与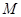 ,与
,与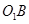 的延长线交于点
的延长线交于点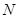 ,当⊙
,当⊙ 的值不变;②
的值不变;②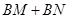 的值不变;
的值不变;


 、
、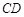 相交于点
相交于点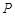 ,若
,若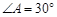 ,
,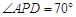 ,则
,则 等于( )
等于( )