ЬтФПФкШн
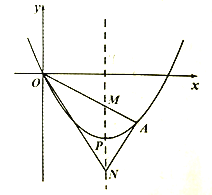
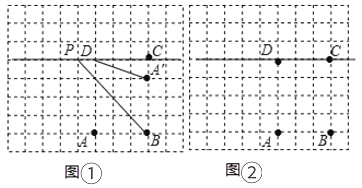
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮABCDЕФБпABдкxжсЩЯЃЌЕуBзјБъЃЈЉ3ЃЌ0ЃЉЃЌЕуCзјБъЃЈ0ЃЌ4ЃЉЃЌЕуPДгдЕуOГіЗЂЃЌвдУПУывЛИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЁмtЁм5ЃЉУыЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпlЃЌжБЯпlЩЈЙ§ЫФБпаЮOCDAЕФУцЛ§ЮЊSЃЎ
ЃЈ1ЃЉЧѓжБЯпADЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕБSЃН![]() ЪБЃЌЧыжБНгаДГіtЕФжЕЃЛ
ЪБЃЌЧыжБНгаДГіtЕФжЕЃЛ
ЃЈ3ЃЉШчЙћЕуMЪЧЃЈ2ЃЉжаЕФжБЯп1ЩЯЕФЕуЃЌЕуNдкxжсЩЯЃЌВЂЧввдAЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧыжБНгаДГіЕуNЕФзјБъЃЎ
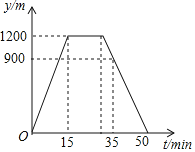
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() xЉ
xЉ![]() ЃЛЃЈ2ЃЉtЕФжЕЮЊ4УыЃЛЃЈ3ЃЉЕуNзјБъЮЊЃЈ1ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЛђЃЈ7ЃЌ0ЃЉЃЎ
ЃЛЃЈ2ЃЉtЕФжЕЮЊ4УыЃЛЃЈ3ЃЉЕуNзјБъЮЊЃЈ1ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЛђЃЈ7ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉдкRtЁїBOCжаЃЌРћгУЙДЙЩЖЈРэМЦЫуBCЕФГЄЃЌМДСтаЮЕФБпГЄЮЊ5ЃЌПЩЕУDКЭAЕФзјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈПЩНтД№ЃЛ
ЃЈ2ЃЉЂйШчЭМ1жаЃЌЕБ0ЁмtЁм2ЪБЃЌжБЯпlЩЈЙ§ЕФЭМЯѓЪЧЫФБпаЮCCQPЃЌSЃН4tЃЎЂкШчЭМ2жаЃЌЕБ2ЃМtЁм5ЪБЃЌжБЯпlЩЈЙ§ЕФЭМаЮЪЧЮхБпаЮOCQTAЃЎЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉИљОнЬтвтЗжШ§жжЧщаЮЗжБ№зїЭМЃЌИљОнЦНааЫФБпаЮЕФаджЪМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпЕуBзјБъЃЈЉ3ЃЌ0ЃЉЃЌЕуCзјБъЃЈ0ЃЌ4ЃЉЃЌ
ЁрOBЃН3ЃЌOCЃН4ЃЌ
дкRtЁїBOCжаЃЌBCЃН![]() ЃН
ЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрCDЃНABЃНBCЃН5ЃЌ
ЁрAЃЈ2ЃЌ0ЃЉЃЌDЃЈ5ЃЌ4ЃЉЃЌ
ЩшADЕФНтЮіЪНЮЊЃКyЃНkx+bЃЌ
дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК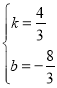 ЃЌ
ЃЌ
ЁржБЯпADЕФКЏЪ§БэДяЪНЮЊЃКyЃН![]() xЉ
xЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйШчЭМ1жаЃЌЕБ0ЁмtЁм2ЪБЃЌжБЯпlЩЈЙ§ЕФЭМЯѓЪЧЫФБпаЮOCQPЃЌSЃН4tЃЎ
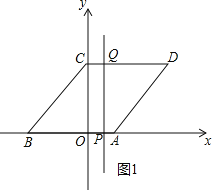
4tЃН![]() ЃЌtЃН
ЃЌtЃН![]() ЃО2ЃЌВЛЗћКЯЬтвтЃЛ
ЃО2ЃЌВЛЗћКЯЬтвтЃЛ
ЂкШчЭМ2жаЃЌЕБ2ЃМtЁм5ЪБЃЌжБЯпlЩЈЙ§ЕФЭМаЮЪЧЮхБпаЮOCQTAЃЎ
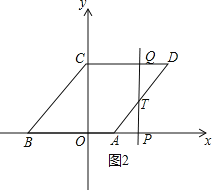
дђOPЃНtЃЌ
tanЁЯOBCЃНtanЁЯPATЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌPTЃН
ЃЌPTЃН![]() ЃЌ
ЃЌ
SЃНSОиаЮCOPQЉSЁїATPЃН4tЉ![]() ЁСЃЈtЉ2ЃЉЁС
ЁСЃЈtЉ2ЃЉЁС![]() ЃЈtЉ2ЃЉЃНЉ
ЃЈtЉ2ЃЉЃНЉ![]() t2+
t2+![]() tЉ
tЉ![]() ЃЌ
ЃЌ
ЕБSЃН![]() ЪБЃЌЉ
ЪБЃЌЉ![]() t2+
t2+![]() tЉ
tЉ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУЃКtЃН4Лђ6ЃЈЩсЃЉЃЌ
злЩЯЃЌЕБSЃН![]() ЪБЃЌtЕФжЕЮЊ4УыЃЛ
ЪБЃЌtЕФжЕЮЊ4УыЃЛ
ЃЈ3ЃЉДцдкШ§жжЧщПіЃК
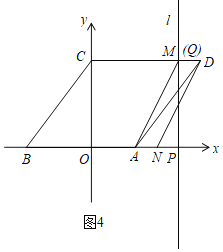
ЂйШчЭМ3жаЃЌЫФБпаЮMNADЪЧЦНааЫФБпаЮЃЌДЫЪБMгыQжиКЯЃЌдђDMЃНANЃЌ
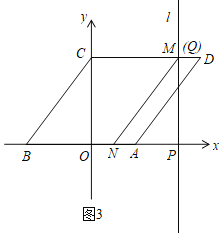
гЩЃЈ2ЃЉжЊЃКtЃН4ЃЌдђCMЃНOPЃН4ЃЌ
ЁрANЃНDMЃН5Љ4ЃН1ЃЌ
ЁрONЃН2Љ1ЃН1ЃЌ
ЁрNЃЈ1ЃЌ0ЃЉЃЛ
ЂкШчЭМ4ЃЌЫФБпаЮANDMЪЧЦНааЫФБпаЮЃЌдђDMЃНANЃЌЭЌРэЕУNЃЈ3ЃЌ0ЃЉЃЛ
ЂлШчЭМ5ЃЌЫФБпаЮADNMЪЧЦНааЫФБпаЮЃЌдђADЃНMNЃН5ЃЌ
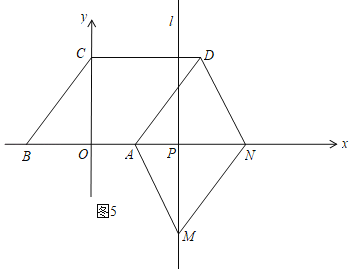
ЁпPMЃН4ЃЌ
RtЁїPMNжаЃЌPNЃН![]() =
=![]() =3ЃЌ
=3ЃЌ
ЁрONЃН4+3ЃН7ЃЌ
ЁрNЃЈ7ЃЌ0ЃЉЃЛ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуNзјБъЮЊЃЈ1ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЛђЃЈ7ЃЌ0ЃЉЃЎ