题目内容
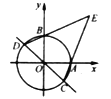
【题目】 已知∠BAC=36°,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是顶角为36°的等腰三角形,即∠A1B1A2=∠A2B2A3=∠A3B3A4=…=∠AnBnAn+1=36°,点A1,A2,A3,…,An在射线AC上,点B1,B2,B3,…,Bn在射线AB上,若A1A2=1,则线段A2018A2019的长为______.

【答案】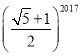
【解析】
先证明△A2B1A1∽△A2AB1,设AA1=A1B1=B1A2=x,则有![]() =
=![]() ,从而可求出x的值,同理可得A2A3的长,A3A4的长,…,根据规律可得出结果.
,从而可求出x的值,同理可得A2A3的长,A3A4的长,…,根据规律可得出结果.
解:∵∠A=∠A1B1A2=36°,A1B1=A2B1,
∴∠AA2B1=∠B1A1A2=72°,
∴∠A=∠AB1A1=36°,
∴AA1=A1B1=B1A2,△A2B1A1∽△A2AB1,
设AA1=A1B1=B1A2=x,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=![]() (舍去负根),
(舍去负根),
同理可得:AA2=A2B2=B2A3=1+![]() ,
,
设A2A3=y,
∵△A3B2A2∽△A3AB2,
∴![]() =
=![]() ,
,
∴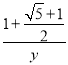 =
=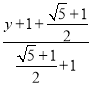 ,
,
解得:y=![]() ,即A2A3=
,即A2A3=![]() ,
,
同理可得:A3A4=(![]() )2,…
)2,…
∴A2018A2019的长=(![]() )2017,
)2017,
故答案为: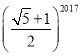 .
.

【题目】为参加 2020 年“陕西省初中毕业升学体育与健康考试”,小强同学进行了刻苦的训练.他在练习立定跳远时,测得其中 10 次立定跳远的成绩(单位:m)如下表:
成绩 | 2.25 | 2.33 | 2.35 | 2.41 | 2.42 |
次数 | 2 | 3 | 2 | 2 | 1 |
这 10 个数据的众数、中位数依次是( )
A.2.35,2.35B.2.33, 2.35C.3, 2.34D.2.33,2.34
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?