题目内容
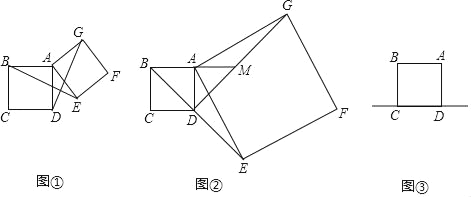
【题目】已知正方形ABCD的边长为2,作正方形AEFG(A,E,F,G四个顶点按逆时针方向排列),连接BE、GD,
(1)如图①,当点E在正方形ABCD外时,线段BE与线段DG有何关系?直接写出结论;
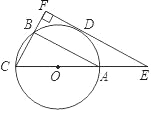
(2)如图②,当点E在线段BD的延长线上,射线BA与线段DG交于点M,且DG=2DM时,求边AG的长;
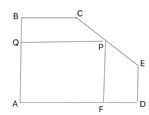
(3)如图③,当点E在正方形ABCD的边CD所在的直线上,直线AB与直线DG交于点M,且DG=4DM时,直接写出边AG的长.
【答案】(1)结论:BE=DG,BE⊥DG.理由见解析;(2)AG=2![]() ;(3)满足条件的AG的长为2
;(3)满足条件的AG的长为2![]() 或2
或2![]() .
.
【解析】
(1)结论:BE=DG,BE⊥DG.只要证明△BAE≌△DAG(SAS),即可解决问题;
(2)如图②中,连接EG,作GH⊥AD交DA的延长线于H.由A,D,E,G四点共圆,推出∠ADO=∠AEG=45°,解直角三角形即可解决问题;
(3)分两种情形分别画出图形即可解决问题;
(1)结论:BE=DG,BE⊥DG.
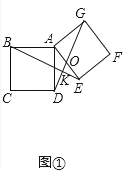
理由:如图①中,设BE交DG于点K,AE交DG于点O.
∵四边形ABCD,四边形AEFG都是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
∴△BAE≌△DAG(SAS),
∴BE=DG,∴∠AEB=∠AGD,
∵∠AOG=∠EOK,
∴∠OAG=∠OKE=90°,
∴BE⊥DG.
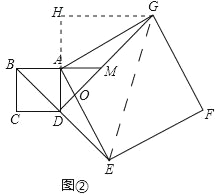
(2)如图②中,连接EG,作GH⊥AD交DA的延长线于H.
∵∠OAG=∠ODE=90°,
∴A,D,E,G四点共圆,
∴∠ADO=∠AEG=45°,
∵∠DAM=90°,
∴∠ADM=∠AMD=45°,
∴![]()
∵DG=2DM,
∴![]()
∵∠H=90°,
∴∠HDG=∠HGD=45°,
∴GH=DH=4,
∴AH=2,
在Rt△AHG中,![]()
(3)①如图③中,当点E在CD的延长线上时.作GH⊥DA交DA的延长线于H.
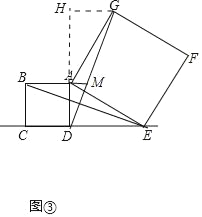
易证△AHG≌△EDA,可得GH=AB=2,
∵DG=4DM.AM∥GH,
∴![]()
∴DH=8,
∴AH=DH﹣AD=6,
在Rt△AHG中, ![]()
②如图3﹣1中,当点E在DC的延长线上时,易证:△AKE≌△GHA,可得AH=EK=BC=2.
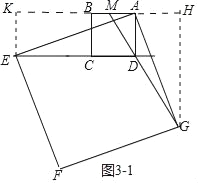
∵AD∥GH,
∴![]()
∵AD=2,
∴HG=10,
在Rt△AGH中, ![]()
综上所述,满足条件的AG的长为![]() 或
或![]() .
.

【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表,请根据图表中提供的信息解答下列问题:
AQI指数 | 质量等级 | 天数(天) |
0-50 | 优 | m |
51-100 | 良 | 44 |
101-150 | 轻度污染 | n |
151-200 | 中度污染 | 4 |
201-300 | 重度污染 | 2 |
300以上 | 严重污染 | 2 |

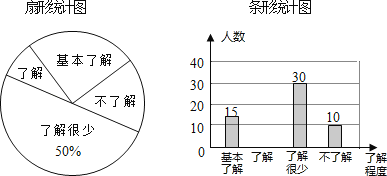
(1)统计表中m= ,n= ,扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少?