题目内容
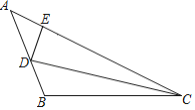
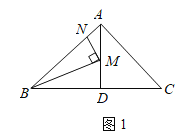
【题目】已知等腰△ABC中，底边BC＝20，D为AB上一点，且CD＝16，BD＝12，则△ABC的周长为____．
【答案】
【解析】
由BC=20，CD=16，BD=12，计算得出BD2+DC2=BC2，根据勾股定理的逆定理即可证明CD⊥AB，设AD=x，则AC=x+12，在Rt△ACD中，利用勾股定理求出x，得出AC，继而可得出△ABC的周长．
解：在△BCD中，BC=20，CD=16，BD=12，
∵BD2+DC2=BC2，
∴△BCD是直角三角形，∠BDC=90°，
∴CD⊥AB，
设AD=x，则AC=x+12，
在Rt△ADC中，∵AC2=AD2+DC2，
∴x2+162=（x+12）2，
解得：x=
．
∴△ABC的周长为：（+12）×2+20=．
故答案为：．
练习册系列答案
相关题目
【题目】某单位要印刷“市民文明出行，遵守交通安全”的宣传材料．甲印刷厂提出：每份材料收1元印刷费，另收150元的制版费；乙印刷厂提出：每份材料收2.5元印刷费，不收制版费．设在同一家印刷厂一次印制数量为
份(为正整数)．
(1)根据题意，填写下表：
一次印制数量(份) | 5 | 10 | 20 | … |
|
甲印刷厂收费(元) | 155 | … | |||
乙印刷厂收费(元) | 12.5 | … |
(2)在印刷品数量大于800份的情况下选哪家印刷厂印制省钱？
