题目内容
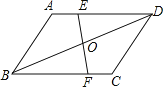
【题目】如图,四边形ABCD是平行四边形,AB=5,BC=10,顶点A在y轴上,边BC在x轴上,且点B的坐标为(﹣4,0)
(1)求点D的坐标;
(2)设点P是边BC上(不与点B、C重合)的一个动点,设点P的坐标为(m,0),△ABP的面积为S,求△ABP的面积S关于m的函数关系式,并写出自变量m的取值范围;
(3)直接写出当△ABP为等腰三角形时点P的坐标.

【答案】(1)点D的坐标为(10,3);(2)![]() (
(![]() );(3)点P的坐标为(4,0)或(1,0)或(﹣
);(3)点P的坐标为(4,0)或(1,0)或(﹣![]() ,0).
,0).
【解析】
(1)根据勾股定理求出OA,根据平行四边形的性质求出点D的坐标;
(2)分点P在OB上和点P在OC上两种情况,根据三角形的面积公式计算即可;
(3)分AB=AP、AB=BP、AP=BP三种情况,根据等腰三角形的性质、勾股定理解答.
(1)∵点B的坐标为(﹣4,0)
∴OB=4,
∴OA=![]() ,
,
∵AD=BC=10,
∴点D的坐标为(10,3);
(2)![]() (
(![]() ),
),
则![]() 关于m的函数关系式为:
关于m的函数关系式为:![]() (
(![]() );
);

(3)当AB=AP时,OP=OB=4,
则点P的坐标为(4,0),
当AB=BP=5时,OP=BP﹣OB=1,
则点P的坐标为(1,0),
如图,当AP=BP时,BP=AP=OB﹣OP=4﹣OP,
由勾股定理得,OP2+OA2=AP2,即(4﹣OP)2=32+OP2,
解得,OP=![]() ,
,
则点P的坐标为(﹣![]() ,0),
,0),
综上所述,当△ABP为等腰三角形时点P的坐标为(4,0)或(1,0)或(﹣![]() ,0).
,0).

【题目】声音在空气中传播的速度![]() (简称音速)与气温
(简称音速)与气温![]() 的关系如下表:
的关系如下表:
气温 | 0 | 5 | 10 | 15 | 20 |
音速 | 331 | 334 | 337 | 340 | 343 |
(1)这一变化过程中,自变量和因变量各是什么?
(2)音速![]() 与气温
与气温![]() 之间的关系式.
之间的关系式.
(3)气温![]()
![]() 时,某人看到烟花燃放
时,某人看到烟花燃放![]() 后才听到声音,那么此人与燃放烟花的所在地约相距多远?
后才听到声音,那么此人与燃放烟花的所在地约相距多远?