题目内容
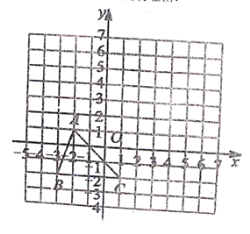
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=﹣1是对称轴,有下列判断:
①b﹣2a=0;②4a﹣2b+c<0;③a﹣b+c=﹣9a;④若(﹣3,y1),( ![]() ,y2)是抛物线上两点,则y1>y2 , 其中正确的是( )
,y2)是抛物线上两点,则y1>y2 , 其中正确的是( )
A.①②③
B.①③④
C.①②④
D.②③④
【答案】B
【解析】解:∵抛物线的对称轴是直线x=﹣1,
∴﹣ ![]() =﹣1,
=﹣1,
b=2a,
∴b﹣2a=0,
故①正确;
∵抛物线的对称轴是直线x=﹣1,和x轴的一个交点是(2,0),
∴抛物线和x轴的另一个交点是(﹣4,0),
∴把x=﹣2代入得:y=4a﹣2b+c>0,
故②错误;
∵图象过点(2,0),代入抛物线的解析式得:4a+2b+c=0,
又∵b=2a,
∴c=﹣4a﹣2b=﹣8a,
∴a﹣b+c=a﹣2a﹣8a=﹣9a,
故③正确;
根据图象,可知抛物线对称轴的右边y随x的增大而减小,
∵抛物线和x轴的交点坐标是(2,0)和(﹣4,0),抛物线的对称轴是直线x=﹣1,
∴点(﹣3,y1)关于对称轴的对称点的坐标是((1,y1),
∵( ![]() ,y2),1<
,y2),1< ![]() ,
,
∴y1>y2,
故④正确;
即正确的有①③④,
所以答案是:B.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.

 天天向上口算本系列答案
天天向上口算本系列答案【题目】某地某一时刻的地面温度是26℃,每升高![]() ,温度下降6℃,下面是温度(℃)与距离地面的高度
,温度下降6℃,下面是温度(℃)与距离地面的高度![]() 对应的数值:
对应的数值:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
|
| … |
根据上表,请完成下面的问题.
(1)表中![]() ;
;
(2)直接写出温度![]() 与高度
与高度![]() 之间的函数关系式,并写出其中的常量和变量;
之间的函数关系式,并写出其中的常量和变量;
(3)求该地距地面![]() 处的温度.
处的温度.