题目内容
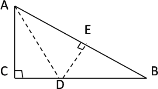
【题目】如图，在ABCD中，EF过对角线的交点O，且与边AB、CD分别相交于点E、F，AB＝5，AD＝3，OF＝1.5，则四边形BCFE的周长为_____．
【答案】11
【解析】
由四边形ABCD是平行四边形，可得OA=OC，AB∥CD，则可证得△AOE≌△COF(ASA)，继而证得OE=OF，进而可得EF=2OE=3，BE+CF=AB=5，继而求出四边形的周长．
∵四边形ABCD是平行四边形，
∴AB∥CD，OA=OC，BC=AD=3，
∴∠OCF=∠OAE，
在△AOE和△COF，
，
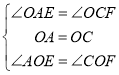∴△AOE≌△COF(ASA)，
∴AE=CF，EF=2OF=2×1.5=3，
∴四边形BCFE的周长为：EF+CF+BC+BE=EF+BC+AE+BE=EF+BC+AB=5+3+3=11，
故答案为：11．
练习册系列答案
相关题目
【题目】某地某一时刻的地面温度是26℃，每升高
，温度下降6℃，下面是温度（℃）与距离地面的高度
对应的数值：
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
|
| … |
根据上表，请完成下面的问题．
（1）表中
；
（2）直接写出温度
与高度
之间的函数关系式，并写出其中的常量和变量；
（3）求该地距地面
处的温度．
