题目内容
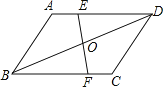
【题目】已知:如图,在ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.
(1)求证:OE=OF;
(2)连接BE、DF,若BD平分∠EBF,试判断四边形EBFD的形状,并给予证明.
【答案】(1)详见解析;(2)四边形EBFD是菱形
【解析】
(1)连接BE、DF,证明四边形EBFD为平行四边形,根据平行四边形的性质即可求解.
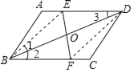
(2)根据BD平分∠EBF,可得∠1=∠2,由平行线的性质可得∠3=∠2,等量代换可得∠1=∠3,即可证明BE=ED,即可判定四边形EBFD的形状.
解:(1)证明:连接BE、DF,
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴OE=OF;
(2)解:四边形EBFD是菱形.理由如下:
∵BD平分∠EBF,
∴∠1=∠2,
∵AD∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴BE=ED,
∴平行四边形EBFD是菱形.

练习册系列答案
相关题目
【题目】某商场用13000元购进甲、乙两种矿泉水共400箱,矿泉水的成本价与销售价如下表所示:
类别 | 成本价/(元·箱 | 销售价/(元·箱 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这400箱矿泉水,可获利多少元?