题目内容
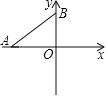
【题目】已知:在平面直角坐标系xOy中,点A、B的坐标分别为(3,0),(0,4),点C(t,0)是x轴上一动点,点M是BC的中点.
(1)当点C和点A重合时,求OM的长;
(2)若S△ACB=10,则t的值为 ;
(3)在(2)的条件下,直线AM交y轴于点N,求△ABN的面积.


【答案】(1)![]() ;(2)t=8或t=-2;(3)当t=8时,△ABN的面积为15,当t=-2时,△ABN的面积为
;(2)t=8或t=-2;(3)当t=8时,△ABN的面积为15,当t=-2时,△ABN的面积为![]() .
.
【解析】
(1)当点C和点A重合时,则OM为Rt△OAB斜边上的中线,根据勾股定理求出AB即可算出;
(2)由题知AC=|t-3|,再根据S△ACB=![]() 列出方程解出t即可;
列出方程解出t即可;
(3)分别讨论当t=8时,当t=-2时,写出M坐标即可求出MA的直线解析式从而求出面积即可.
(1)∵点A、B的坐标分别为(3,0),(0,4),
∴OA=3,OB=4,
∴![]() ,
,
当点C和点A重合时,则OM为Rt△OAB斜边上的中线,则OM=![]() ;
;
(2)由题知AC=|t-3|,S△ACB=![]() ,
,
∴![]()
![]()
![]()
![]() 或
或![]()
t=8或t=-2;
(3)当t=8时,C(8,0),
∵点M是BC的中点,
∴M(4,2),
把M(4,2),A(3,0)代入![]() 中得
中得![]() ,解得:
,解得:![]() ,
,
则![]() ,当x=0时,y=-6,所以N(0,-6),
,当x=0时,y=-6,所以N(0,-6),
则S△ABN=(4+6)×3÷2=15;
当t=-2时,C(-2,0),
∵点M是BC的中点,
∴M(-1,2),
把M(-1,2),A(3,0)代入![]() 中得
中得![]() ,解得:
,解得: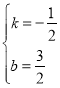 ,
,
则![]() ,当x=0时,y=
,当x=0时,y=![]() ,所以N(0,
,所以N(0,![]() ),
),
则S△ABN=(4-![]() )×3÷2=
)×3÷2=![]() ;
;
综上所述,当t=8时,△ABN的面积为15,当t=-2时,△ABN的面积为![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目