题目内容
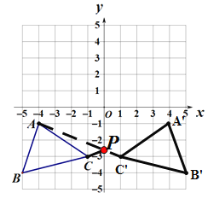
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-4,-1),B(-5,-4),C(-1,-3).

(1)画△A'B'C',使△A'B'C'与△ABC关于y轴对称;
(2)在y轴上作一点P,使得PA+PC最短;
(3)将△ABC向右平移m个单位,向上平移n个单位,若点A落在第二象限内,且点C在第四象限内,则m的范围是 ,n的范围是 .
【答案】(1)见详解;(2)见详解;(3)![]() ,
,![]() .
.
【解析】
(1)利用关于y轴对称点的性质得出各对应点位置,进而得出答案;
(2)由(1)点C'是点C关于y轴的对称点,连接A C',与y轴相交于点P,点P为所求;
(3)根据题意,由点A为(![]() 4,
4,![]() 1),点C为(
1),点C为(![]() 1,
1,![]() 3),结合平移的规则,有点A平移后的坐标为(
3),结合平移的规则,有点A平移后的坐标为(![]() );点C平移后的坐标为(
);点C平移后的坐标为(![]() ); 然后联合成不等式组,即可得到m、n的取值范围.
); 然后联合成不等式组,即可得到m、n的取值范围.
解:(1)如图所示;
(2)连接A C',与y轴相交于点P,点P为所求;
(3)根据题意,
∵点A为(![]() 4,
4,![]() 1),点C为(
1),点C为(![]() 1,
1,![]() 3),
3),
∴点A平移后的坐标为:(![]() );
);
∴点C平移后的坐标为:(![]() );
);
∵点A落在第二象限内,且点C在第四象限内,
∴![]() ,
,![]() ,
,
解得:![]() ,
,![]() ;
;
故答案为:![]() ;
;![]() .
.

练习册系列答案
相关题目