题目内容
【题目】如图,AB是半圆O的直径,C是半圆O上一点,OQ⊥BC于点Q,过点B作半圆O的切线,交OQ的延长线于点P,PA交半圆O于R,则下列等式中正确的是( )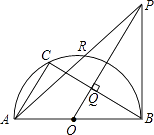
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:(1)连接AQ,如图1,
∵BP与半圆O切于点B,AB是半圆O的直径,
∴∠ABP=∠ACB=90°.
∵OQ⊥BC,
∴∠OQB=90°.
∴∠OQB=∠OBP=90°.
又∵∠BOQ=∠POB,
∴△OQB∽△OBP.
∴ ![]() .
.
∵OA=OB,
∴ ![]() .
.
又∵∠AOQ=∠POA,
∴△OAQ∽△OPA.
∴∠OAQ=∠APO.
∵∠OQB=∠ACB=90°,
∴AC∥OP.
∴∠CAP=∠APO.
∴∠CAP=∠OAQ.
∴∠CAQ=∠BAP.
∵∠ACQ=∠ABP=90°,
∴△ACQ∽△ABP.
∴ ![]() .
.
故A正确.
2)如图1,
∵△OBP∽△OQB,
∴ ![]() .
.
∴ ![]() .
.
∵AQ≠OP,
∴ ![]() .
.
故C不正确.
3)连接OR,如图2所示.
∵OQ⊥BC,
∴BQ=CQ.
∵AO=BO,
∴OQ= ![]() AC.
AC.
∵OR= ![]() AB.
AB.
∴ ![]() =
= ![]() ,
, ![]() =2.
=2.
∴ ![]() ≠
≠ ![]() .
.
∴ ![]() .
.
故B不正确.
4)如图2,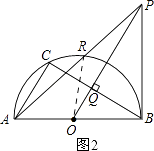
∵ ![]() ,
,
且AC=2OQ,AB=2OB,OB=OR,
∴ ![]() .
.
∵AB≠AP,
∴ ![]() .
.
故D不正确.
故选:A.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半)的相关知识才是答题的关键.

练习册系列答案
相关题目