题目内容
【题目】已知，如图，抛物线y=ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB． 
（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．
【答案】
（1）解：∵B（1，0），
∴OB=1；
∵OC=3BO，
∴C（0，﹣3）；
∵y=ax2+3ax+c过B（1，0）、C（0，﹣3），
∴ 
；
解这个方程组，得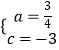 
，
∴抛物线的解析式为：y= 
x2+ 
x﹣3
（2）解：过点D作DM∥y轴分别交线段AC和x轴于点M、N
在y= x2+ x﹣3中，令y=0，
得方程 x2+ x﹣3=0解这个方程，得x1=﹣4，x2=1
∴A（﹣4，0）
设直线AC的解析式为y=kx+b
∴ 
，
解这个方程组，得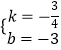 
，
∴AC的解析式为：y=﹣ x﹣3，
∵S四边形ABCD=S△ABC+S△ADC
= 
+ 
DM（AN+ON）
= +2DM
设D（x， x2+ x﹣3），M（x，﹣ x﹣3），DM=﹣ x﹣3﹣（ x2+ x﹣3）=﹣ （x+2）2+3，
当x=﹣2时，DM有最大值3
此时四边形ABCD面积有最大值 
．
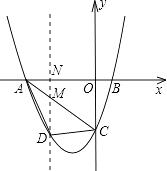
【解析】（1）已知了B点坐标，易求得OB、OC的长，进而可将B、C的坐标代入抛物线中，求出待定系数的值，即可得出抛物线的解析式．（2）根据A、C的坐标，易求得直线AC的解析式．由于AB、OC都是定值，则△ABC的面积不变，若四边形ABCD面积最大，则△ADC的面积最大；可过D作x轴的垂线，交AC于M，x轴于N；得△ADC的面积是DM与OA积的一半，可设出N点的坐标，分别代入直线AC和抛物线的解析式中，即可求出DM的长，进而可得出四边形ABCD的面积与N点横坐标间的函数关系式，根据所得函数的性质即可求出四边形ABCD的最大面积．
【考点精析】根据题目的已知条件，利用二次函数的性质的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
