题目内容
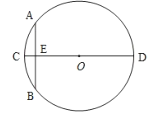
【题目】如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.

(1)求∠DAE的度数;
(2)求BP的长.
【答案】(1)求∠DAE=22.5°;(2)BP=1
【解析】
(1)由正方形得到∠ACB=45°,![]() ,由AC=EC,根据等腰三角形的等边对等角的性质,及三角形外角的性质得到∠E=22.5°,依据平行线的性质即可得到∠DAE的度数;
,由AC=EC,根据等腰三角形的等边对等角的性质,及三角形外角的性质得到∠E=22.5°,依据平行线的性质即可得到∠DAE的度数;
(2)由正方形得到AB=1,∠DAB=90°,∠DBC=45°,依据三角形外角的性质得到∠APB=∠E+∠DBC=67.5°,而∠BAP=90°-22.5°=67.5°,故而∠BAP=∠APB,依据三角形等角对等边的性质即可求得BP的长.
解:(1)∵四边形ABCD的正方形,
∴∠ACB=45°,![]() ,
,
∵AC=EC,
∴∠E=∠EAC,
又∵∠ACB=∠E+∠EAC=45°,
∴∠E=22.5°,
∵![]() ,
,
∴∠DAE=∠E=22.5°;
(2)∵四边形ABCD是正方形,正方形ABCD的边长是1,
∴AB=1,∠DAB=90°,∠DBC=45°,
∵∠DAE=22.5°,
∴∠BAP=90°-22.5°=67.5°,∠APB=∠E+∠DBC=22.5°+45°=67.5°,
∴∠BAP=∠APB,
∴BP=AB=1.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】某市中招体育测试改革,其中篮球和足球作为选考项目,某商店抓住这一商机决定购进一批篮球和足球共200个,这两种球的进价和售价如下表所示:
篮球 | 足球 | |
进价(元/个) | 180 | 150 |
售价(元/个) | 250 | 200 |
(1)若商店计划销售完这批球后能获利11600元,问篮球和足球应分别购进多少个?
(2)设购进篮球![]() 个,获利为
个,获利为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(3)若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元,请问有哪几种购球方案,并写出获利最大的购球方案.