题目内容
【题目】已知点A(1,2)为反比例函数![]() 图象上一点,
图象上一点,
(1) 将点A沿x轴正方向平移1个单位,对应点A′的坐标为___________
将比例函数![]() 图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
将比例函数![]() 图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
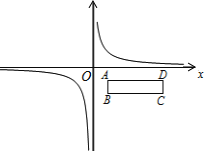
(2) 在平面直角坐标系中,矩形ABCD位置如图,其中A、B、C三点的坐标分别为A(1,-1)、B(1,-2)、C(4,-2).现将反比例函数![]() 图象沿x轴正方向平移,若平移速度为每秒1个单位长度
图象沿x轴正方向平移,若平移速度为每秒1个单位长度
① 设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
② 在平移过程中,当函数图象与矩形ABCD有公共点时,则函数图象扫过的区域夹在直线AD、BC的图形面积为___________(直接写出答案)
【答案】(1)(1) A′(2,2);![]() ;
;![]() ;(2)① 2≤t≤6;②4
;(2)① 2≤t≤6;②4
【解析】(1)根据坐标平移的性质,横坐标的平移:左减右加,纵坐标的平移:上加下减,直接求解即可.
(2)①通过(1)的平移变化,设经过时间t后的解析式,由通过B、D两个临界点求出t的范围;
②由题意可知证明扫过的区域为平行四边形,然后求出面积即可.
(1) 根据平移的性质可得:A′(2,2)
由平移的性质可得:![]()
同理可得: ![]()
(2) ① 经过时间t后反比例函数的解析式为![]()
当函数图象经过点B时,![]() ,解得t=2
,解得t=2
当函数图象经过点D时,![]() ,解得t=6
,解得t=6
∴2≤t≤6
② 平行四边形,长为4,高为1,那么面积为4.

 寒假学与练系列答案
寒假学与练系列答案【题目】一个水果市场某品种苹果的销售方式如下表:
购买苹数量(千克) | 不超过 | 超过 |
每千克的价格(元) |
|
|
(1)如果小明购买![]() 千克的苹果,那么他需要付___________元.
千克的苹果,那么他需要付___________元.
(2)小明分两次共购买![]() 千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付
千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付![]() 元,求他两次分别购买苹果的数量.
元,求他两次分别购买苹果的数量.
【题目】无锡某学校准备组织学生及学生家长到南京大学参观体验,为了便于管理,所有人员到南京必须乘坐在同一列动车上;根据报名人数,若都买一等座单程火车票需5032元,若都买二等座单程火车票且花钱最少,则需2970元;已知学生家长人数是教师人数的2倍,无锡到南京的动车票价格(动车学生票只有二等座可以打6折)如下表所示:
运行区间 | 票价 | ||
上车站 | 下车站 | 一等座 | 二等座 |
无锡 | 南京 | 68(元) | 55(元) |
(1)参加参观体验的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加体验的人数),其余的需买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买单程火车票的总费用至少是多少钱?最多是多少钱?