题目内容
如下图,在Rt△ABC中,∠ACB=900,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为


A. | B. | C. | D. |
C。
如图,过C作CM⊥AB,交AB于点M,

由垂径定理可得M为AD的中点,
∵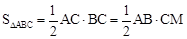 ,且AC=3,BC=4,AB=5,
,且AC=3,BC=4,AB=5,
∴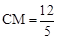 。
。
在Rt△ACM中,根据勾股定理得: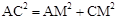 ,
,
∴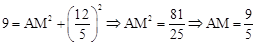 (舍去负值)。
(舍去负值)。
∴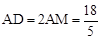 。故选C。
。故选C。

由垂径定理可得M为AD的中点,
∵
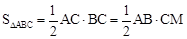 ,且AC=3,BC=4,AB=5,
,且AC=3,BC=4,AB=5,∴
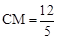 。
。在Rt△ACM中,根据勾股定理得:
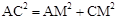 ,
,∴
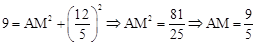 (舍去负值)。
(舍去负值)。∴
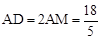 。故选C。
。故选C。
练习册系列答案
相关题目

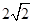 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;
 ,求⊙O的直径.
,求⊙O的直径.

 ,BD=1,求△DEC外接圆的直径.
,BD=1,求△DEC外接圆的直径.



 ,则这个圆锥的侧面积是
,则这个圆锥的侧面积是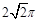
 中,
中, ,
, .
.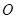 是
是 的中点,⊙
的中点,⊙ 与点
与点 .与
.与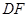 并延长交
并延长交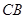 的延长线于点
的延长线于点 .若
.若 ,则
,则 __.
__.