题目内容
【题目】在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）
如图，已知AB∥CD，BE、CF分别平分∠ABC和∠DCB，求证：BE∥CF．
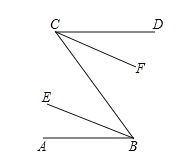
证明：∵AB∥CD，（已知）
∴∠_______=∠_______．___________________________
∵__________________________________________，（已知）
∴∠EBC=_______，（角平分线定义）
同理，∠FCB=______________．
∴∠EBC=∠FCB．（等式性质）
∴BE//CF．（_____________________________________）
【答案】ABC DCB 两直线平行，内错角相等 BE平分∠ABC ∠ABC ∠DCB 内错角相等，两直线平行
【解析】
根据平行线的性质得出∠ABC=∠DCB，求出∠EBC=∠FCB，根据平行线的判定得出即可．
∵AB∥CD（已知）
∴∠ABC=∠DCB（两直线平行，内错角相等）．
∵BE平分∠ABC（已知），∴∠EBC
∠ABC（角平分线的定义）
同理：∠FCB∠DCB，∴∠FBC=∠FCB（等式性质），∴BE∥CF（内错角相等，两直线平行）．
故答案为：ABC；DCB；两直线平行，内错角相等；BE平分∠ABC；∠ABC；∠DCB；内错角相等，两直线平行．
练习册系列答案
优学名师名题系列答案
相关题目
