题目内容
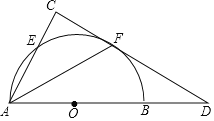
【题目】已知:如图,△ABC是等边三角形,点D是平面内一点,连接CD,将线段CD绕C顺时针旋转60°得到线段CE,连接BE,AD,并延长AD交BE于点P.
(1)当点D在图1所在的位置时
①求证:△ADC≌△BEC;
②求∠APB的度数;
③求证:PD+PE=PC;
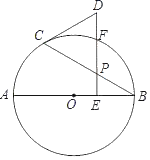
(2)如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.

【答案】(1)①见解析;②∠APB=60°;③见解析;(2)当∠ADC=90°时,CE取最大值为2![]() .
.
【解析】
(1)①根据旋转的性质和等边三角形的性质以及全等三角形的判定证明即可;
②根据全等三角形的判定和性质以及三角形内角和解答即可;
③根据等边三角形的性质以及全等三角形的判定和性质解答即可;
(2)当∠ADC=90°时,CE取最大值,进而利用直角三角形的性质解答即可.
(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,
∵将线段CD绕C顺时针旋转60°得到线段CE,
∴CE=CD,∠DCE=60°,
∴△DCE是等边三角形,
∴∠DCE=60°,
∵∠ACD+∠DCB=60°,∠BCE+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS);
②∵△ACD≌△BCE,
∴∠EBC=∠DAC,
∵∠DAC+∠BAD=∠BAC=60°,
∴∠PBC+∠BAD=60°,
∴∠APB=180°﹣∠ABC+∠PBC+∠BAP=180°﹣60°﹣60°=60°;
③∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠CAD+∠BAD=60°,∠BAD+∠DBC=60°,
∴∠BAD+∠ABD=∠BDP=60°,
∵∠APB=60°,
∴△BDP是等边三角形,
∴DP=BP,
∴PD+PE=BE,
∵△ADC≌△BEC,
∴AD=BE,
∵在△ABD与△CBP中
 ,
,
∴△ABD≌△CBP(SAS),
∴AD=PC,
∴PD+PE=PC;
(2)当∠ADC=90°时,CE取最大值,
∵AB=AC=4,AD=2,
∴CD=![]() ,
,
∴CE=2![]() ,
,
即当∠ADC=90°时,CE取最大值为2![]() .
.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案【题目】某景点的门票价格如表
购票人数/人 | 1~40 | 41~80 | 80以上 |
每人门票价/元 | 10 | 8 | 6 |
某校九年级(1)、(2)两班计划去春游该景点,其中(1)班人数少于40人,(2)班人数多于40人且少于80人,如果两班都以班为单位单独购票,则一共支付838元:如果两班联合起来作为一个团体购票,则只需花费570元
(1)两个班各有多少名学生;
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
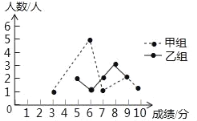
【题目】某校举行了一次古诗词朗读竞赛,满分为10分,学生得分均为整数,成绩达到6分及6分以上为合格.达到9分或10分为优秀.这次竞赛中,甲、乙两组学生成绩统计分析表和成绩分布的折线统计图如图所示.
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优率率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出成绩统计分析表中a的值.
(2)小英说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察成绩统计分析表判断,小英是甲、乙哪个组的学生.
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.试写出两条支持乙组同学观点的理由.
(4)从这次参加学校古诗词朗诵竞赛的甲、乙两组成绩优秀的学生中,随机抽取两名学生参加全市古诗词朗诵竞赛,恰好是乙组学生的概率是多少?(画树状图或列表求解)