题目内容
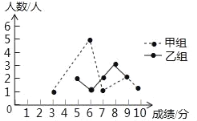
【题目】某校举行了一次古诗词朗读竞赛,满分为10分,学生得分均为整数,成绩达到6分及6分以上为合格.达到9分或10分为优秀.这次竞赛中,甲、乙两组学生成绩统计分析表和成绩分布的折线统计图如图所示.
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优率率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出成绩统计分析表中a的值.
(2)小英说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察成绩统计分析表判断,小英是甲、乙哪个组的学生.
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.试写出两条支持乙组同学观点的理由.
(4)从这次参加学校古诗词朗诵竞赛的甲、乙两组成绩优秀的学生中,随机抽取两名学生参加全市古诗词朗诵竞赛,恰好是乙组学生的概率是多少?(画树状图或列表求解)
【答案】(1)中位数a=6;(2)小英属于甲组学生;(3)①乙组的总体平均水平高;②乙组的成绩比甲组的成绩稳定;(4)随机抽取两名学生参加全市古诗词朗诵竞赛,恰好是乙组学生的概率为![]() .
.
【解析】
(1)由折线图中数据,根据中位数的定义求解可得;
(2)根据中位数的意义求解可得;
(3)可从平均数和方差两方面阐述即可;
(4)首先根据题意列表,然后求得所有等可能的结果与两名学生恰好是乙组的情况,再利用概率公式即可求得答案.
(1)由折线统计图可知,甲组成绩从小到大排列为:3、6、6、6、6、6、7、9、9、10,
∴其中位数a=6,
(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩位于小组中上游,
∴小英属于甲组学生;
(3)乙组学生成绩的平均分b=(5×2+6×1+7×2+8×3+9×2)÷10=7.2;
①乙组的平均分高于甲组,即乙组的总体平均水平高;
②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定;
(4)列表得:
甲1 | 甲2 | 甲3 | 乙1 | 乙2 | |
甲1 | (甲2,甲1) | (甲3,甲1) | (乙1,甲1) | (乙2,甲1) | |
甲2 | (甲1,甲2) | (甲3,甲2) | (乙1,甲2) | (乙2,甲2) | |
甲3 | (甲1,甲3) | (甲2,甲3) | (乙1,甲3) | (乙2,甲3) | |
乙1 | (甲1,乙1) | (甲 | (甲3,乙1) | (乙2,乙1) | |
乙2 | (甲1,乙2) | (甲2,乙2) | (甲3,乙2) | (乙1,乙2) |
∵共有20种等可能的结果,两名学生恰好是乙组的有2种情况,
∴随机抽取两名学生参加全市古诗词朗诵竞赛,恰好是乙组学生的概率=![]() .
.

【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B |
| 0.25 |
C | 16 | b |
D | 8 |
|
合计 | a | 1 |
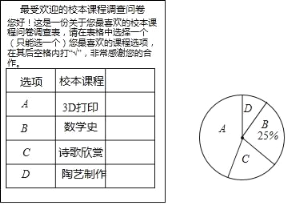
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
【题目】某学校八年级学生学习《从数据谈节水》后,积极响应“节约用水,从我做起”的号召,下列是10名学生统计各自家族一个月的节水情况:
节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
家族数(个) | 1 | 2 | 2 | 4 | 1 |
那么这组数据的众数和中位数分别是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()